Áp dụng tỉ số lượng giác trong tam giác MBO để tính số đo góc MBO, từ đó tính được số đo góc MBN. Lời giải bài tập, câu hỏi Giải bài 22 trang 109 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Tiếp tuyến của đường tròn. Cho đường tròn (O; R) và điểm A nằm trên đường tròn….
Đề bài/câu hỏi:
Cho đường tròn (O; R) và điểm A nằm trên đường tròn. Lấy điểm B sao cho A là trung điểm của đoạn thẳng OB. Kẻ hai tiếp tuyến BM, BN của đường tròn (O).
a) Tính số đo góc MBN và độ dài đoạn thẳng BM theo R.
b) Tứ giác AMON là hình gì ? Vì sao?
c) Tính độ dài đoạn thẳng OH theo R với H là giao điểm của OA và MN.
Hướng dẫn:
a) Áp dụng tỉ số lượng giác trong tam giác MBO để tính số đo góc MBO, từ đó tính được số đo góc MBN.
Tính BM: Áp dụng định lý Pythagore trong tam giác OBM.
b) Chứng minh 2 tam giác AMO và ANO đều.
c) Áp dụng tỉ số lượng giác trong tam giác MHO để tính OH.
Lời giải:
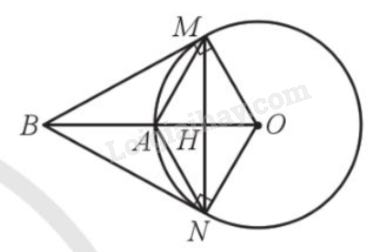
a) Ta có A là trung điểm của đoạn thẳng OB nên \(OB = 2OA = 2R\).
Do BM, BN là 2 tiếp tuyến của (O) nên \(MO \bot BM,NO \bot BN\) hay \(\widehat {BMO} = \widehat {BNO} = 90^\circ \) và \(\widehat {MBO} = \widehat {NBO} = \frac{{\widehat {MBN}}}{2}\); \(\widehat {MOB} = \widehat {NOB}\).
Xét tam giác MBO vuông tại M có
\(\sin \widehat {MBO} = \frac{{MO}}{{BO}} = \frac{R}{{2R}} = \frac{1}{2}\), do đó \(\widehat {MBO} = 30^\circ \).
Ta có \(\widehat {MBO} = \frac{{\widehat {MBN}}}{2}\) hay \(\widehat {MBN} = 2\widehat {MBO} = 2.30^\circ = 60^\circ \).
Áp dụng định lý Pythagore trong tam giác vuông OBM có:
\(BM = \sqrt {B{O^2} – M{O^2}} = \sqrt {{{\left( {2R} \right)}^2} – {R^2}} = R\sqrt 3 \)
b) Xét tam giác vuông MOB có \(\widehat {MBO} = 30^\circ \) nên \(\widehat {MOB} = 90^\circ – \widehat {MBO} = 90^\circ – 30^\circ = 60^\circ \)
Mà \(\widehat {MOB} = \widehat {NOB}\) nên \(\widehat {NOB} = 60^\circ \).
Xét tam giác AMO có \(AO = MO\left( { = R} \right)\) và \(\widehat {MOB} = 60^\circ \) nên tam giác AMO đều, suy ra \(AM = MO\).
Xét tam giác ANO có \(AO = NO\left( { = R} \right)\) và \(\widehat {NOB} = 60^\circ \) nên tam giác ANO đều, suy ra \(AN = NO\).
Mà \(OM = ON\left( { = R} \right)\) nên \(OM = ON = AM = AN\).
Vậy AMON là hình thoi.
c) Vì AMON là hình thoi nên 2 đường chéo AO và MN vuông góc với nhau.
Xét tam giác vuông MHO ta có:
\(\cos \widehat {MOH} = \frac{{OH}}{{MO}}\) hay \(OH = \cos \widehat {MOH}.MO = \cos 60^\circ .R = \frac{R}{2}\).