Dựa vào dữ kiện đề bài để vẽ hình. Dựa vào đa giác đều là đa giác có tất cả các cạnh bằng nhau và. Trả lời Giải bài 10 trang 108 sách bài tập toán 9 – Cánh diều tập 2 – Bài 1. Đa giác đều. Hình đa giác đều trong thực tiễn. Cho tam giác đều ABC cạnh a. Vẽ về phía ngoài tam giác ABC các hình chữ nhật ABEF,…
Đề bài/câu hỏi:
Cho tam giác đều ABC cạnh a. Vẽ về phía ngoài tam giác ABC các hình chữ nhật ABEF, BCIJ và CAGH sao cho AF = BJ = CH = x. Tìm hệ thức liên hệ giữa a2 và x2 để hình lục giác EFGHIJ là lục giác đều.
Hướng dẫn:
Dựa vào dữ kiện đề bài để vẽ hình.
Dựa vào đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải:
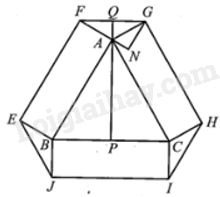
Gọi P là trung điểm của BC và Q là giao điểm của các đường thẳng AP và FG.
Xét ∆ABC đều có AP là đường trung tuyến nên đồng thời là đường phân giác của tam giác.
Do đó: \(\widehat {BAP} = \widehat {PAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}{.60^o} = {30^o}\).
Xét ∆AFG cân tại A (do AF = AG = x) nên đường trung tuyến AQ đồng thời là đường phân giác của tam giác. Do đó \(\widehat {FAG} = 2\widehat {PAQ}\).
Lại có: \(\widehat {PAQ} + \widehat {FAB} + \widehat {BAP} = {180^o}\)
Nên \(\widehat {PAQ} = {180^o} – \widehat {FAB} – \widehat {BAP}\) \( = {180^o} – {90^o} – {30^o} = {60^o}\).
Suy ra \(\widehat {PAG} = 2.\widehat {PAQ} = {2.60^o} = {120^o}\).
Kẻ GN vuông góc với FA (N thuộc FA).
Tam giác FQA vuông tại Q có \(\widehat {FAQ} = {60^o}\) và FA = x nên ta có:
\(FQ = FA.\sin \widehat {FAQ} = \frac{{x\sqrt 3 }}{2}\), do đó FG = 2FQ = \(x\sqrt 3 \).
Do ABEF, BCIJ và CAGH là các hình chữ nhật nên ta có: AB = EF, BC = IJ, CA = GH, mà AB = BC = CA (do ∆ABC đều) nên nếu EFGHIJ là lục giác đều thì FG = GH = AC = a, do đó a = \(x\sqrt 3 \) hay a2 = 3x2.
Ngược lại, nếu a2 = 3x2 thì FG = a và các cạnh của lục giác EFGHIJ bằng nhau. (1)
Ta có \(\widehat {AFQ} + \widehat {FAQ} = {90^o}\) (do ∆AFQ vuông tại Q) nên:
\(\widehat {AFQ} = {90^o} – \widehat {FAQ} = {90^o} – {60^o} = {30^o}\)
Suy ra \(\widehat {EFQ} = \widehat {EFA} + \widehat {AFQ} = {90^o} + {30^o} = {120^o}\).
Tương tự, ta chứng minh được các góc của lục giác EFGHIJ đều bằng 120° nên lục giác EFGHIJ là lục giác đều.
Vậy hệ thức liên hệ giữa a2 và x2 để lục giác EFGHIJ là lục giác đều là a2 = 3x2.