Sử dụng giả thiết để tạo ra các đơn thức và đa thức cần tìm. Sử dụng công thức tính diện tích hình tròn. Lời giải bài tập, câu hỏi Giải bài 5 trang 15 vở thực hành Toán 8 – Luyện tập chung trang 13. Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét….
Đề bài/câu hỏi:
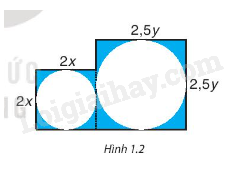
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimét và y centimét. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimét) như hình bên. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
Hướng dẫn:
– Sử dụng giả thiết để tạo ra các đơn thức và đa thức cần tìm.
– Sử dụng công thức tính diện tích hình tròn: \(S = \pi {r^2}\)
– Diện tích phần còn lại = diện tích miếng bìa – diện tích hai hình tròn cắt ra.
Lời giải:
Miếng bìa gồm có hai hình vuông có cạnh lần lượt là \(2x\) và \(2,5y\) ghép lại.
Do đó diện tích của miếng bìa là \(2x.2x + 2,5y.2,5y = 4{x^2}\; + 6,25{y^2}.\)
Tổng diện tích hai hình tròn cắt ra là \({\left( {2x} \right)^2}.\pi + {\left( {2,5y} \right)^2}.\pi = 4\pi {x^2}\; + 6,25\pi {y^2}.\)
Vậy diện tích phần còn lại của miếng bìa là:
\((4{x^2}\; + 6,25{y^2}) – (4\pi {x^2}\; + 6,25\pi {y^2}) = 4\left( {1 – \pi } \right){x^2}\; + 6,25\left( {1 – \pi } \right){y^2}.\)
Đó là đa thức bậc 2.