Sử dụng tính chất đường trung bình của tam giác. Sử dụng dấu hiệu nhận biết hình chữ nhật. Hướng dẫn giải Giải bài 4 trang 74 vở thực hành Toán 8 – Bài 16. Đường trung bình trong tam giác. Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H,…
Đề bài/câu hỏi:
Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật.
Hướng dẫn:
– Sử dụng tính chất đường trung bình của tam giác.
– Sử dụng dấu hiệu nhận biết hình chữ nhật.
Lời giải:
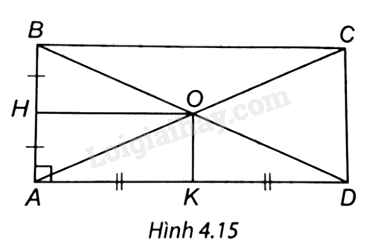
(H.4.15). ∆ABD có: H là trung điểm AB, O là trung điểm BD (do tứ giác ABCD là hình chữ nhật) nên HO là đường trung bình của ∆ABD.
Suy ra HO // AD và \(HO = \frac{1}{2}AD\).
Xét tứ giác AHOK: HO // AK và HO = AK nên tứ giác AHOK là hình bình hành.
Ta có \(\widehat {HAK} = 90^\circ \) nên tứ giác AHOK là hình chữ nhật.