Trả lời Luyện tập 3 Bài 34. Ba trường hợp đồng dạng của hai tam giác (trang 88, 89) – SGK Toán 8 Kết nối tri thức. Tham khảo: Chứng minh ΔABC ∽ ΔADB (g. g) suy ra tỉ số đồng dạng.
Câu hỏi/Đề bài:
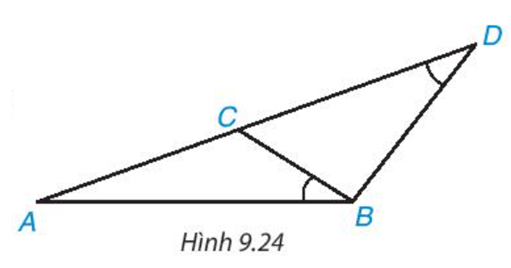
Cho các điểm A, B, C, D như Hình 9.24. Biết rằng \(\widehat {ABC} = \widehat {A{\rm{D}}B}\). Hãy chứng minh ΔABC ∽ ΔADB và \(A{B^2} = A{\rm{D}}.AC\)
Hướng dẫn:
Chứng minh ΔABC ∽ ΔADB (g.g) suy ra tỉ số đồng dạng
Lời giải:
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)