Hướng dẫn giải Luyện tập 2 Bài 39. Hình chóp tứ giác đều (trang 119) – SGK Toán 8 Kết nối tri thức. Tham khảo: Tính thể tích không khí trong lều bằng công thức tính thể tích của hình chóp tứ giác đều.
Câu hỏi/Đề bài:
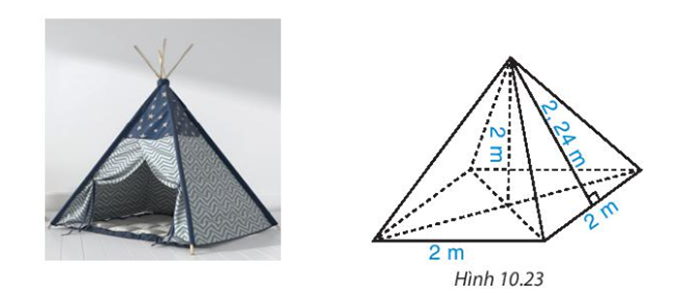
Một chiếc lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 2 m, chiều cao bằng 2 m
a) Thể tích không khí trong lều là bao nhiêu?
b) Biết lều phủ vải bốn phía và cả mặt tiếp đất. Tính diện tích vải bạt cần dùng (coi mép nối không đáng kể), biết rằng người ta đo chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m.
Hướng dẫn:
– Tính thể tích không khí trong lều bằng công thức tính thể tích của hình chóp tứ giác đều.
– Diện tích bạt vải cần dùng là: Sxq + Sđ
Lời giải:
a) Có diện tích đáy lều là: 2.2=4 (m2)
Thể tích không khí trong lều là: \(V = \frac{1}{3}.S.h = \frac{1}{3}.4.2 = \frac{8}{3}\left( {{m^3}} \right)\)
b) Nửa chu vi đáy lều là: (2.4):2=4 (m)
– Có \({S_{xq}} = p.d = 4.2,24 = 8,96({m^2})\)
=> Diện tích bạt vải cần dùng là: Sxq + Sđ = 8,96 + 4 = 12,96 (m2)