Chứng minh tứ giác DEKI có các cặp cạnh đối song song với nhau nên DEKI là hình bình hành. Phân tích và giải Giải bài 9 trang 136 SGK Toán 8 tập 2 – Kết nối tri thức – Bài tập ôn tập cuối năm. Cho tam giác ABC. Các đường trung tuyến AF, BE và CD cắt nhau tại G….
Đề bài/câu hỏi:
Cho tam giác ABC. Các đường trung tuyến AF, BE và CD cắt nhau tại G. Gọi I, K theo thứ tự là trung điểm của BG và CG
a) Chứng minh rằng tứ giác DEKI là hình bình hành
b) Biết AF = 6cm. Tính độ dài các đoạn thẳng DI và EK
Hướng dẫn:
a) Chứng minh tứ giác DEKI có các cặp cạnh đối song song với nhau nên DEKI là hình bình hành.
b) Sử dụng tính chất trọng tâm của tam giác.
Lời giải:
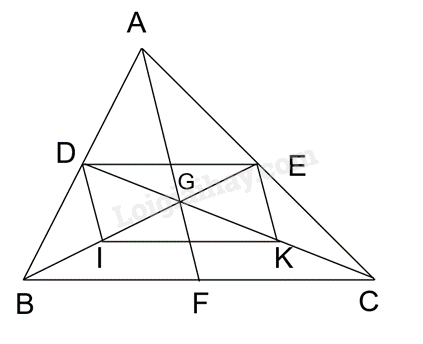
Xét tam giác ABC có:
D là đường trung tuyến của AB
E là đường trung tuyến của AC
=> DE là đường trung bình của tam giác ABC
=> DE // BC (1)
Tương tự, có IK là đường trung bình của tam giác GBC
=> IK // BC (2)
=> DE // IK (3)
– Có ID là đường trung bình của tam giác ABG => ID // AG
EK là đường trung bình của tam giác ACG => EK // AG
=> ID // EK (4)
Từ (3) và (4) => DEIK là hình bình hành
b) Có điểm G là trọng tâm của tam giác ABC => \(AG = \frac{2}{3}{\rm{AF}}\)=> AG = 4cm
=> \(DI = EK = \frac{1}{2}AG = 2cm\)