Chứng minh hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có: \(\widehat {NBO} = \widehat {OM{\rm{A}}}\. Gợi ý giải Giải bài 9.25 trang 103 SGK Toán 8 tập 2 – Kết nối tri thức – Bài 36. Các trường hợp đồng dạng của hai tam giác vuông. Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox,…
Đề bài/câu hỏi:
Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh tam giác OAM đồng dạng với tam giác OBN.
Hướng dẫn:
Chứng minh hai tam giác vuông OBN (vuông tại N) và tam giác OAM (vuông tại M) có: \(\widehat {NBO} = \widehat {OM{\rm{A}}}\)
Lời giải:
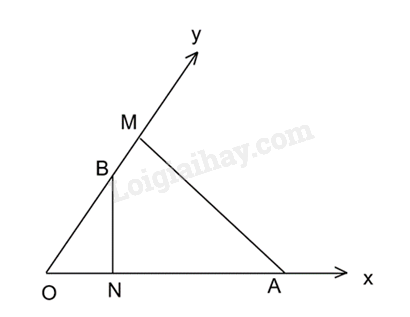
Xét tam giác OAM và tam giác OBN có:
\(\widehat{ONB}= \widehat{OMA}=90°\)
góc O chung
Suy ra ΔOAM ∽ ΔOBN