Chứng minh\(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\) Chứng minh ΔAED ∽ ΔBEC (c. g. Vận dụng kiến thức giải Giải bài 9.15 trang 92 SGK Toán 8 tập 2 – Kết nối tri thức – Luyện tập chung trang 91. Cho các điểm A, B, C, D, E như Hình 9.30….
Đề bài/câu hỏi:
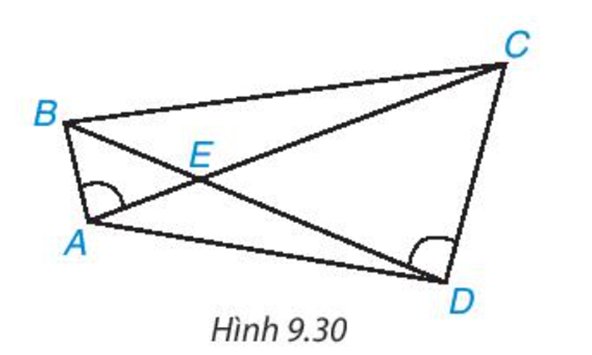
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Hướng dẫn:
– Chứng minh\(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
– Chứng minh ΔAED ∽ ΔBEC (c.g.c)
Lời giải:
Xét hai tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {C{\rm{D}}B}\)(giả thiết)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra \(\Delta A{\rm{E}}B \backsim \Delta DEC\) (g.g) suy ra:
\(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Xét hai tam giác AED và BEC có:
\(\widehat {A{\rm{ED}}} = \widehat {BEC}\) (đối đỉnh)
\(\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Suy ra ΔAED ∽ ΔBEC (c.g.c)