Bài 9.13 trang 92 Toán 8 tập 2 – Kết nối tri thức: Cho hình thang ABCD (AB // CD) có ∠ DAB = ∠ DBC a) Chứng minh rằng ΔABD ∽ ΔBDC b) Giả sử AB=2cm, AD=3cm, BD=4cm

Đề bài/câu hỏi:

Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)

a) Chứng minh rằng ΔABD ∽ ΔBDC

b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC

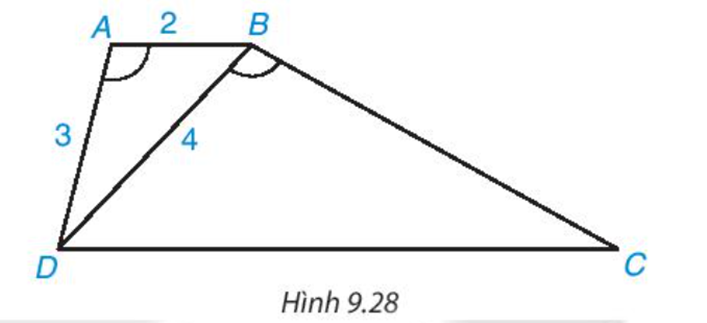
Hướng dẫn:

a) Chứng minh ΔABD ∽ ΔBDC (g.g)

b) Tính tỉ số đồng dạng của tam giác ABD và tam giác BDC. Từ đó tính độ dài của DC, BC

Lời giải:

a) Có AB // CD Suy ra \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}\)

– Xét ΔABD và ΔBDC

Có \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}{,^{}}\widehat {DAB} = \widehat {DBC}\)

Suy ra ΔABD ∽ ΔBDC (g.g)

b) Có \(\frac{{AB}}{{B{\rm{D}}}} = \frac{{12}}{{24}} = \frac{1}{2}\)

ΔABD ∽ ΔBDC với tỉ số \(\frac{1}{2}\)

Suy ra \(\frac{3}{{BC}} = \frac{4}{{DC}} = \frac{1}{2}\)

Suy ra BC=6 (cm)

DC=8 (cm)