Bài 3 trang 114 Toán 8 tập 1 – Kết nối tri thức: Phân tích các đa thức sau thành nhân tử: a) x^4 – 4x^3 – 7x^2 + 8x + 10b) x + y + z ^3 – x^3 – y^3 – z^3

Đề bài/câu hỏi:

Phân tích các đa thức sau thành nhân tử:

\(\begin{array}{l}a){x^4} – 4{{\rm{x}}^3} – 7{{\rm{x}}^2} + 8{\rm{x}} + 10\\b){\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3}\end{array}\)

Hướng dẫn:

Sử dụng lệnh Factor() (hoặc Factorise()).

Lời giải:

a) Phân tích các đa thức \({x^4} – 4{{\rm{x}}^3} – 7{{\rm{x}}^2} + 8{\rm{x}} + 10\)thành nhân tử:

• Sử dụng lệnh Factor() (hoặc Factorise()).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

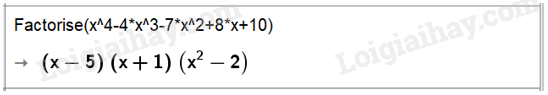
Vậy \({x^4} – 4{{\rm{x}}^3} – 7{{\rm{x}}^2} + 8{\rm{x}} + 10 = \left( {x – 5} \right)\left( {x + 1} \right)\left( {{x^2} – 2} \right)\)

b) Phân tích các đa thức \({\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3}\) thành nhân tử:

• Sử dụng lệnh Factor() (hoặc Factorise()).

• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy \({\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3} = 3\left( {y + z} \right)\left( {x + z} \right)\left( {x + y} \right)\)