Áp dụng tính chất tia phân giác của một góc và định lí tổng các góc trong một tứ giác. Giải chi tiết Giải bài 3.37 trang 73 SGK Toán 8 tập 1 – Kết nối tri thức – Luyện tập chung trang 73. Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy…
Đề bài/câu hỏi:
Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
Hướng dẫn:
Áp dụng tính chất tia phân giác của một góc và định lí tổng các góc trong một tứ giác.
Lời giải:
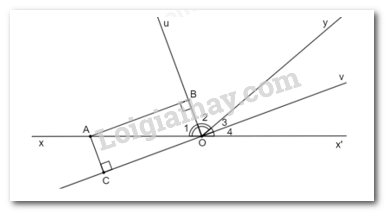
Vì Ou, Ov lần lượt là tia phân giác của \(\widehat {xOy};\widehat {x’Oy}\) nên \(\widehat {{O_1}} = \widehat {{O_2}};\widehat {{O_3}} = \widehat {{O_4}}\)
Mà \(\widehat {xOy} + \widehat {x’Oy} = {180^o}\) (vì \(\widehat {xOy};\widehat {x’Oy}\) là hai góc kề bù).
Hay \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = {180^o}\)
Suy ra \(2\widehat {{O_2}} + 2\widehat {{O_3}} = {180^o}\)
Do đó \(\widehat {{O_2}} + \widehat {{O_3}} = {90^o}\) hay \(\widehat {uOv} = {90^o}\) suy ra \(\widehat {uOC} = {90^o}\) hay \(\widehat {BOC} = {90^o}\)
Vì B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov
Nên \(\widehat {ABO} = {90^o};\widehat {AC{\rm{O}}} = {90^o}\)
Tứ giác OBAC có \(\widehat {AC{\rm{O}}} + \widehat {BOC} + \widehat {ABO} + \widehat {BAC} = {360^o}\)
\({90^o} + {90^o} + {90^o} + \widehat {BAC} = {360^o}\)
270°+\(\widehat {BAC} = {360^o}\)
Suy ra \(\widehat {BAC}\)=360°−270°=90o
Xét tứ giác OBAC có \(\widehat {BOC} = {90^o};\widehat {ABO} = {90^o};\widehat {AC{\rm{O}}} = {90^o}\)
Vậy tứ giác OBAC là hình chữ nhật.