Xét 3 trường hợp có thể xảy ra: Nếu A là đỉnh đối của D Nếu B là đỉnh đối của D Nếu C là. Hướng dẫn giải Giải bài 3.24 trang 63 SGK Toán 8 tập 1 – Kết nối tri thức – Luyện tập chung trang 62. Cho ba điểm không thẳng hàng….
Đề bài/câu hỏi:
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.
b) Hỏi tìm được bao nhiêu điểm như vậy?
Hướng dẫn:
Xét 3 trường hợp có thể xảy ra:
– Nếu A là đỉnh đối của D
– Nếu B là đỉnh đối của D
– Nếu C là đỉnh đổi của D
=> Ta được các hình bình hành tương ứng.
Lời giải:
a) Gọi ba điểm không thẳng hàng đó là A, B, C. Khi đó ta cần tìm điểm D để bốn điểm A, B, C, D là 4 đỉnh của hình bình hành. Gọi (H) là hình bình hành cần tìm.
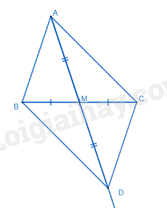
+ TH1. Nếu A là đỉnh đối của D trong (H), khi đó trung điểm của AD trùng với trung điểm của BC.
Gọi M là trung điểm của BC. Ta có M cũng là trung điểm của AD. Trên tia đối của tia MA lấy điểm D sao cho AM = MD, ta được hình bình hành ABDC là (H).
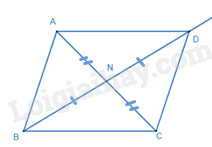
+ TH2. Nếu B là đỉnh đối của D trong (H), khi đó trung điểm của BD trùng với trung điểm của AC.
Gọi N là trung điểm của AC. Ta có N cũng là trung điểm của BD. Trên tia đối của tia NB lấy điểm D sao cho BN = ND, ta được hình bình hành ABCD là (H).
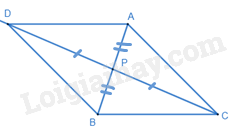
+ TH3. Nếu C là đỉnh đối của D trong (H), khi đó trung điểm của CD trùng với trung điểm của AB.
Gọi P là trung điểm của AB. Ta có P cũng là trung điểm của CD. Trên tia đối của tia PC lấy điểm D sao cho CP = PD, ta được hình bình hành ACBD là (H).
b) Theo phần a, ta thấy có 3 điểm D thỏa mãn yêu cầu bài toán.
Khi D là đỉnh đối của A thì ta có hình bình hành ABDC.
Khi D là đỉnh đối của B thì ta có hình bình hành ABCD.
Khi D là đỉnh đối của A thì ta có hình bình hành ACBD.