Chứng minh AMCN là hình bình hành. Sử dụng tính chất của hình bình hành để giải. Lời giải Giải bài 3.20 trang 63 SGK Toán 8 tập 1 – Kết nối tri thức – Luyện tập chung trang 62. Cho hình bình hành ABCD….
Đề bài/câu hỏi:
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM;
b) \(\widehat {AMC} = \widehat {ANC}\)
Hướng dẫn:
Chứng minh AMCN là hình bình hành. Sử dụng tính chất của hình bình hành để giải.
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
Lời giải:
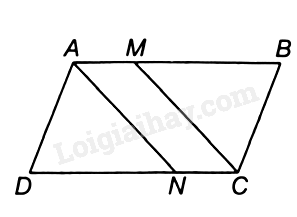
a) Vì ABCD là hình bình hành nên AB // CD.
Tứ giác AMCN có AM // CN (vì AB // CD); AM = CN (giả thiết).
Suy ra, tứ giác AMCN là hình bình hành.
Do đó AN = CM (đpcm).
b) Vì tứ giác AMCN là hình bình hành suy ra \(\widehat {AMC} = \widehat {ANC}\) (đpcm).