Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\. Hướng dẫn giải Giải bài 12 trang 136 SGK Toán 8 tập 2 – Kết nối tri thức – Bài tập ôn tập cuối năm. Cho tam giác ABC không phải là tam giác vuông,…
Đề bài/câu hỏi:
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE \(\backsim\) ΔACF , từ đó suy ra ΔAEF \(\backsim\) ΔABC
b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF
Hướng dẫn:
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\) ΔACF
b) Sử dụng các tỉ số đồng dạng của hai tam giác để tính EF
Lời giải:
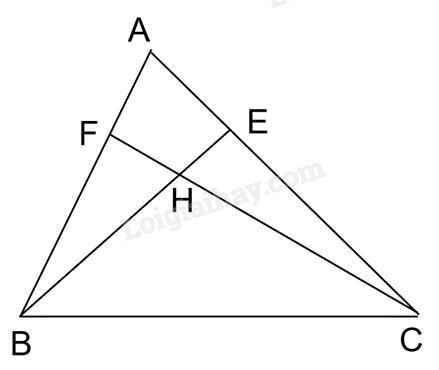
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\) ΔACF
=> \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)
Xét tam giác AEF và tam giác ABC có: A chung và \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)
=> ΔAEF \(\backsim\) ΔABC (c.g.c)
b) Xét tam giác vuông AEB có
=> \(A{{\rm{E}}^2} = A{B^2} – B{E^2}\)
=> \(A{{\rm{E}}^2} = {10^2} – {8^2}\)
=> AE=6 cm
Vì ΔAEF \(\backsim\) ΔABC
=> \(\frac{{A{\rm{E}}}}{{AB}} = \frac{{EF}}{{BC}}\)
=> \(\frac{6}{{10}} = \frac{{EF}}{{15}}\)
=> EF=9 cm