Giải Vận dụng Bài 4. Hai hình đồng dạng (trang 79, 80) – SGK Toán 8 Chân trời sáng tạo. Gợi ý: Hai hình \(H\) và hình \(H’\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình.
Câu hỏi/Đề bài:
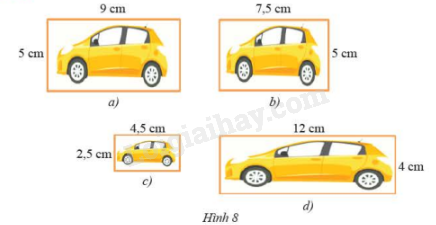
Trong Hình 8b, c, d, Hình nào đồng dạng với Hình 8a. Giải thích.
Hướng dẫn:
Hai hình \(H\) và hình \(H’\) được gọi là đồng dạng nếu có hình đồng dạng phối của của hình \(H\) bằng hình \(H’\).
Lời giải:
– Xét hình 8a và hình 8b ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8b lần lượt là:
\(\frac{9}{{7,5}} = 1,2;\frac{5}{5} = 1\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.
– Xét hình 8a và hình 8c ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8c lần lượt là:
\(\frac{9}{{4,5}} = 2;\frac{5}{{2,5}} = 2\). Do đó, tồn tại hình động dạng phối cảnh của hình 8a bằng hình 8c (hình 8a thu nhỏ với tỉ số 2). Do đó, hình 8a và hình 8c đồng dạng với nhau.
– Xét hình 8a và hình 8d ta có:
Tỉ lệ của chiều dài – chiều dài và chiều rộng – chiều rộng của hình 8a và hình 8d lần lượt là:
\(\frac{9}{{12}} = 0,75;\frac{5}{4} = 1,25\). Do đó, không tồn tại hình động dạng phối cảnh nào của hình 9a để bằng hình 8b. Do đó, hình 8a và hình 8b không đồng dạng với nhau.