Trả lời Vận dụng 4 Bài 3. Hình thang – Hình thang cân (trang 70, 71) – SGK Toán 8 Chân trời sáng tạo. Gợi ý: Chứng minh \(QH = KP\).
Câu hỏi/Đề bài:
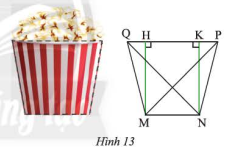
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Hướng dẫn:
Chứng minh \(QH = KP\)
Tính độ dài các đoạn thẳng \(HK\), \(QH\), \(KP\)
Áp dụng định lý Pythagore tính độ dài \(MH\), \(MQ\)
Lời giải:
a) Xét \(\Delta MHQ\) và \(\Delta NKP\) ta có:
\(\widehat {MHQ} = \widehat {NKP} = 90^\circ \)
\(MQ = NP\) (do \(MNPQ\) là hình thang cân)
\(\widehat {MQP} = \widehat {NPQ}\) (do \(MNPQ\) là hình thang cân)
Suy ra: \(\Delta MHQ = \Delta NKP\) (ch – gn)
Suy ra: \(HQ = KP\) (hai cạnh tương ứng)
Suy ra \(HQ = KP = \frac{{PQ – HK}}{2} = \frac{{10 – 6}}{2} = 2\) (cm)
\(HP = 8\)cm
Áp dụng định lý Pythagore vào tam giác vuông \(MHP\) ta có:
\(M{H^2} = M{P^2} – H{P^2} = {\left( {8\sqrt 2 } \right)^2} – {8^2} = 128 – 64 = 64\)
\(MH = 8\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(MHQ\) ta có:
\(M{Q^2} = M{H^2} + Q{H^2} = {8^2} + {2^2} = 68\)
\(MQ = \sqrt {68} \) (cm)