Hướng dẫn giải TH 2 Bài 1. Định lí Thalès trong tam giác (trang 44, 45) – SGK Toán 8 Chân trời sáng tạo. Hướng dẫn: Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Câu hỏi/Đề bài:
Trong Hình 3, chứng minh rằng:
a) \(AB\) và \(BC\) tỉ lệ với \(A’B’\) và \(B’C’\);
b) \(AC\) và \(A’C’\) tỉ lệ với \(AB\) và \(A’B’\).
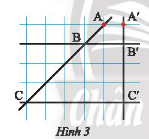
Hướng dẫn:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải:
Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).
Khi đó, độ dài các đoạn thẳng là
\(AB = b;BC = 3b;A’B’ = a;B’C’ = 3a;AC = 4b;A’C’ = 4a\)
a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).
Tỉ số của \(A’B’\) và \(B’C’\) là \(\frac{{A’B’}}{{B’C’}} = \frac{a}{{3a}} = \frac{1}{3}\).
Do đó, \(AB\) và \(BC\) tỉ lệ với \(A’B’\) và \(B’C’\).
b) Tỉ số của \(AC\) và \(A’C’\)là \(\frac{{AC}}{{A’C’}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).
Tỉ số của \(AB\) và \(A’B’\) là \(\frac{{AB}}{{A’B’}} = \frac{b}{a}\).
Do đó, \(AC\) và \(A’C’\) tỉ lệ với \(AB\) và \(A’B’\).