Lời giải Hãy giải bài toán ở phần mở đầu trang 49 – Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều – hình chóp tứ giác đều. Hướng dẫn: Sử dụng công thức tính diện tích toàn phần của hình chóp tam giác đều.
Câu hỏi/Đề bài:
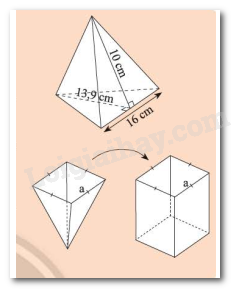
a) Bạn Mai cần dán giấy bóng kính màu xung quanh một chiếc lồng đèn hình chóp tam giác đều với kích thước như hình bên. Hỏi diện tích giấy mà Mai cần là bao nhiêu?
b) Bạn Hùng dùng một cái gàu hình chóp tứ giác đều để múc nước đổ vào một thùng chứa hình lăng trụ có cùng diện tích đáy và chiều cao như hình bên. Hãy dự đoán xem bạn Hùng phải đổ bào nhiêu gàu thì nước đầy thùng.
Hướng dẫn:
a) Sử dụng công thức tính diện tích toàn phần của hình chóp tam giác đều
b) Sử dụng công thức tính thể tích của hình lăng trụ đứng và hình chóp tứ giác đều.
Lời giải:
a) Diện tích xung quanh của chiếc lồng là: \(10.3.16:2 = 240\) (\(c{m^2}\))
Diện tích đáy là: \(13,9.16:2 = 111,2\) (\(c{m^2}\))
Diện tích giấy mai cần là: \(240 + 111,2 = 351,2\) (\(c{m^2}\))
b) Gọi \(h\) là chiều cao của gàu nước và thùng chứa
Thể tích gàu nước là: \(V = \frac{1}{3}{a^2}h\)
Thể tích thùng chứa là: \(V = {a^2}h\)
Bạn Hùng phải đổ số gàu nước là: \({a^2}h:\left( {\frac{1}{3}{a^2}h} \right) = 3\) (gàu)