Học xong bài này chúng ta có thể sử dụng tính chất đường trung bình của tam giác để giải bài toán. Giải chi tiết Giải câu hỏi khởi động trang 52 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 2. Đường trung bình của tam giác. Giữa hai điểm…
Đề bài/câu hỏi:
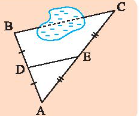
Giữa hai điểm \(B\) và \(C\) có một hồ nước (xem hình bên). Biết \(DE = 45m\). Làm thế nào để tính được khoảng cách giữa hai điểm \(B\) và \(C\)?
Hướng dẫn:
Học xong bài này chúng ta có thể sử dụng tính chất đường trung bình của tam giác để giải bài toán.
Lời giải:
Vì \(BD = DA \Rightarrow D\) là trung điểm của \(AB\);
Vì \(EC = EA \Rightarrow E\) là trung điểm của \(AC\).
Do đó, \(DE\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right. \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)\)
Vậy khoảng các của hai điểm \(B\) và \(C\) là 90 m.