Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau. Trả lời Giải bài 9 trang 72 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 2. Các trường hợp đồng dạng của hai tam giác. Trong Hình 21a, cho biết…
Đề bài/câu hỏi:
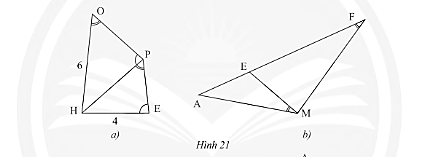
a) Trong Hình 21a, cho biết \(\widehat {HOP} = \widehat {HPE},\widehat {HPO} = \widehat {HEP},OH = 6cm\) và \(HE = 4cm\). Tính độ dài đoạn thẳng \(HP\).
b) Trong Hình 21b, cho biết \(\widehat {AME} = \widehat {AFM}\). Chứng minh rằng \(A{M^2} = AE.AF\).
Hướng dẫn:
– Nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đố đồng dạng với nhau.
– Hai tam giác đồng dạng thì các cặp cạnh tương ứng có cùng tỉ lệ.
Lời giải:
a) Xét tam giác \(OPH\) tam giác \(PEH\) ta có:
\(\widehat {HOP} = \widehat {HPE}\) (giả thuyết)
\(\widehat {OPH} = \widehat {PEH}\) (giả thuyết)
Do đó, \(\Delta OPH\backsim\Delta PEH\) (g.g)
Suy ra, \(\frac{{PH}}{{EH}} = \frac{{OH}}{{PH}} \Rightarrow P{H^2} = OH.EH = 4.6 \Rightarrow P{H^2} = 24 \Leftrightarrow PH = \sqrt {24} = 2\sqrt 6 \).
Vậy \(PH = 2\sqrt 6 \).
b) Xét tam giác \(AME\) tam giác \(AFM\) ta có:
\(\widehat {AME} = \widehat {AFM}\) (giả thuyết)
\(\widehat A\) chung
Do đó, \(\Delta AME\backsim\Delta AFM\) (g.g)
Suy ra, \(\frac{{AM}}{{AF}} = \frac{{AE}}{{AM}} \Rightarrow A{M^2} = AF.AE\) (điều phải chứng minh).