Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo. Phân tích, đưa ra lời giải Giải bài 4 trang 66 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 1. Hai tam giác đồng dạng. Trong Hình 14, cho biết…
Đề bài/câu hỏi:
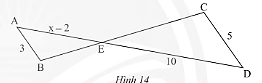
Trong Hình 14, cho biết \(AB//CD\)
a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).
b) Tìm \(x\).
Hướng dẫn:
Nếu một đường thẳng cắt phần kéo dài của hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải:
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x – 2}}{{10}} = \frac{3}{5} \Rightarrow x – 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).