Sử dụng tính chất tổng các góc trong một tứ giác bằng \(360^\circ \. Phân tích, đưa ra lời giải Giải bài 2 trang 66 SGK Toán 8 – Chân trời sáng tạo – Bài 2. Tứ giác. Góc kề bù với một góc của tứ giác…
Đề bài/câu hỏi:
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
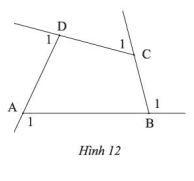
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.
Hướng dẫn:
Sử dụng tính chất tổng các góc trong một tứ giác bằng \(360^\circ \)
Lời giải:
Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ – \widehat {DAB}} \right) + \left( {180^\circ – \widehat {ABC}} \right) + \left( {180^\circ – \widehat {BCD}} \right) + \left( {180^\circ – \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ – \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ – 360^\circ \\\)
\(= 360^\circ \)