Sử dụng Tính chất đường phân giác trong tam giác: Trong tam giác. Hướng dẫn cách giải/trả lời Giải bài 1 trang 56 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 3. Tính chất đường phân giác của tam giác. Tính độ dài…
Đề bài/câu hỏi:
Tính độ dài \(x\) trong Hình 7.
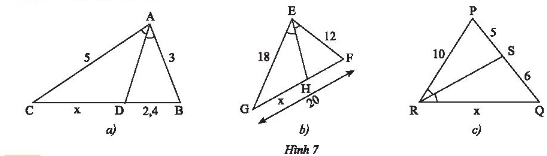
Hướng dẫn:
Sử dụng Tính chất đường phân giác trong tam giác:
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
Lời giải:
a) Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{CD}}{{BD}} = \frac{{AC}}{{AB}} \Leftrightarrow \frac{x}{{2,4}} = \frac{5}{3} \Rightarrow x = \frac{{2,4.5}}{3} = 4\).
Vậy \(x = 4\).
b) Ta có: \(GH + HF = GF \Rightarrow HF = GF – GH = 20 – x\)
Vì \(EH\) là phân giác của góc \(GEF\) nên theo tính chất đường phân giác ta có:
\(\frac{{GH}}{{HF}} = \frac{{GE}}{{EF}} \Leftrightarrow \frac{x}{{20 – x}} = \frac{{18}}{{12}} \Leftrightarrow \frac{x}{{20 – x}} = \frac{3}{2} \Rightarrow 2x = 3.\left( {20 – x} \right)\)
\( \Leftrightarrow 2x = 60 – 3x \Leftrightarrow 5x = 60 \Rightarrow x = 12\)
Vậy \(x = 12\).
c) Vì \(RS\) là phân giác của góc \(RPQ\) nên theo tính chất đường phân giác ta có:
\(\frac{{PS}}{{SQ}} = \frac{{PR}}{{RQ}} \Leftrightarrow \frac{5}{6} = \frac{{10}}{x} \Rightarrow x = \frac{{10.6}}{5} = 12\).
Vậy \(x = 12\).