Lời giải Luyện tập 2 Bài 3. Hình thang cân (trang 102, 103) – SGK Toán 8 Cánh diều. Gợi ý: Quan sát hình 29 sau khi mở rộng thì ô cửa đó có dạng hình thang cân.
Câu hỏi/Đề bài:
Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 m và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô của sổ đó có dạng hình gì? Tính diện tích của ô của sổ đó sau khi mở rộng.
Hướng dẫn:
Quan sát hình 29 sau khi mở rộng thì ô cửa đó có dạng hình thang cân.
Lời giải:
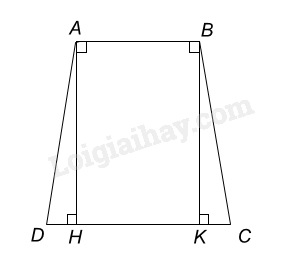
Xét \(\Delta AHD\) và \( \Delta BKC\) có:
\(\widehat {AHD} =\widehat{BKC} = 90^0\)
AH = BK
HD = KC
\( \Rightarrow \Delta AHD = \Delta BKC (c.g.c) \Rightarrow \widehat{ADH} = \widehat{BCK}\)
Do AB // KH hay AB // CD suy ra ABCD là hình thang.
Mà \(\widehat{ADH} = \widehat{BCK}\) (cmt)
Suy ra ABCD là hình thang cân.
Ta có: AB = HK = 80 (cm)
DC = DH + HK + KC = 20 + 80 + 20 = 120 (cm).
Chiều cao của hình thang ABCD là 120 cm (= BK).
=> Diện tích của ô cửa sổ sau khi mở rộng là:
\( S = \frac{1}{2}(AB + CD).BK = \frac{1}{2}(80 + 120).120 = 12000(cm^2)\)