Trả lời Luyện tập 1 Bài 7. Trường hợp đồng dạng thứ hai của tam giác (trang 79, 80) – SGK Toán 8 Cánh diều. Hướng dẫn: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng.
Câu hỏi/Đề bài:
Cho hai tam giác ABC và A’B’C’ thỏa mãn \(AB = 2,AC = 3,A’B’ = 6,A’C’ = 9\) và \(\widehat A = \widehat {A’}\). Chứng minh \(\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}\).
Hướng dẫn:
Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai rồi suy ra các góc bằng nhau theo định nghĩa tam giác đồng dạng.
Lời giải:
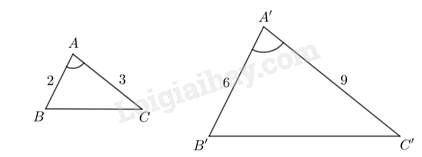
Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A’B’}} = \frac{2}{6} = \frac{1}{3}\\\frac{{AC}}{{A’C’}} = \frac{3}{9} = \frac{1}{3}\\ \Rightarrow \frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\end{array}\)
Xét tam giác ABC và tam giác A’B’C’ có:
\(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\) và \(\widehat A = \widehat {A’}\)
\( \Rightarrow \Delta ABC \backsim \Delta A’B’C’\) (c-g-c)
\( \Rightarrow \)\(\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}\)