Chứng minh \(\widehat {HBC} = \widehat {BAH}\) rồi chứng minh hai tam giác đồng dạng. Gợi ý giải Giải bài 8 trang 95 SGK Toán 8 – Cánh diều – Bài tập cuối chương 8. Cho Hình 105. Chứng minh:…
Đề bài/câu hỏi:
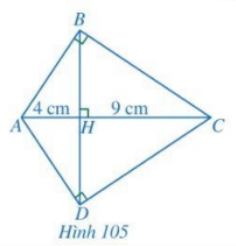
Cho Hình 105. Chứng minh:
a) \(\Delta HAB \backsim \Delta HBC\)
b) \(HB = HD = 6cm\)
Hướng dẫn:
a) Chứng minh \(\widehat {HBC} = \widehat {BAH}\) rồi chứng minh hai tam giác đồng dạng.
b) Tính độ dài HB và HD rồi so sánh với nhau.
Lời giải:
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).