Dựa vào tính chất đường phân giác để suy ra các tỉ lệ tương ứng. Hướng dẫn giải Giải bài 4 trang 94 SGK Toán 8 – Cánh diều – Bài tập cuối chương 8. Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I…
Đề bài/câu hỏi:
Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I. Biết I thuộc đoạn thẳng BD (Hình 103). Chứng minh \(AB.CD = AD.BC\).
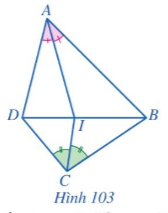
Hướng dẫn:
Dựa vào tính chất đường phân giác để suy ra các tỉ lệ tương ứng.
Lời giải:
Vì AI là đường phân giác của góc DAB nên \(\frac{{ID}}{{IB}} = \frac{{AD}}{{AB}}\) (Tính chất đường phân giác)
Vì CI là đường phân giác của góc BCD nên \(\frac{{ID}}{{IB}} = \frac{{CD}}{{CB}}\) (Tính chất đường phân giác)
\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{CD}}{{CB}} \Rightarrow AB.CD = AD.BC\)