Xác định hai điểm thuộc đồ thị hàm số đã cho. Vẽ đường thẳng đi qua hai điểm ta được đồ thị hàm số. Lời giải bài tập, câu hỏi Giải bài 3 trang 77 SGK Toán 8 tập 1 – Cánh diều – Bài 4. Đồ thị của hàm số bậc nhất y=ax+b(a khác 0). Vẽ đồ thị các hàm số…
Đề bài/câu hỏi:
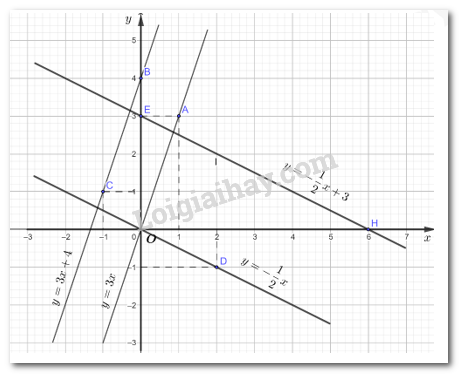
Vẽ đồ thị các hàm số \(y = 3{\rm{x}};y = 3{\rm{x}} + 4;y = – \dfrac{1}{2}x;y = – \dfrac{1}{2}x + 3\) trên cùng một mặt phẳng tọa độ.
Hướng dẫn:
Xác định hai điểm thuộc đồ thị hàm số đã cho. Vẽ đường thẳng đi qua hai điểm ta được đồ thị hàm số.
Lời giải:
* y = 3x
Với x = 1 thì y = 3, ta được điểm A(1; 3) thuộc đồ thị hàm số y = 3x
Vậy đồ thị hàm số y = 3x là đường thẳng đi qua hai điểm O(0; 0) và A(1; 3)
* y = 3x + 4
Với x = 0 thì y = 4, ta được điểm B(0; 4) thuộc đồ thị hàm số y = 3x + 4
Với x = -1 thì y = 1, ta được điểm C(-1; 1) thuộc đồ thị hàm số y = 3x + 4
Vậy đồ thị hàm số y = 3x + 4 là đường thẳng đi qua hai điểm B(0; 4) và C(-1; 1)
* \(y = – \dfrac{1}{2}x\)
Với x = 2 thì y = -1, ta được điểm D(2; -1) thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x\)
Vậy đồ thị hàm số \(y = – \dfrac{1}{2}x\) là đường thẳng đi qua hai điểm O(0; 0) và điểm D(2; -1)
* \(y = – \dfrac{1}{2}x + 3\)
Với x = 0 thì y = 3, ta được điểm E(0; 3) thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Với y = 0 thì x = 6 ta được điểm H(6; 0) thuộc đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\)
Vậy đồ thị hàm số \(y = – \dfrac{1}{2}x + 3\) là đường thẳng đi qua hai điểm E(0; 3) và H(6; 0)