Ta đánh dấu các điểm của các tam giác vuông Áp dụng định lí Pythagore để tính độ dài các cạnh. Hướng dẫn cách giải/trả lời Giải bài 3 trang 100 SGK Toán 8 tập 1 – Cánh diều – Bài 2. Tứ giác. Hình 20 mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thủy….
Đề bài/câu hỏi:
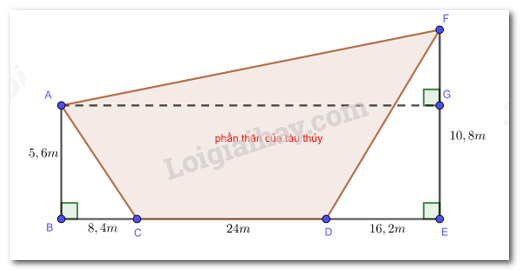
Một chiếc tàu thủy có mặt cắt dọc phần nổi trên mặt nước của tân tàu được mô tả ở Hình 20. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của thân tàu đó (làm tròn kết quả đến hàng phần mười của mét).
Hướng dẫn:
Ta đánh dấu các điểm của các tam giác vuông
Áp dụng định lí Pythagore để tính độ dài các cạnh.
Lời giải:
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE – GE = FE – AB = 10,8 – 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.