Dựa vào tính chất đường phân giác để chứng minh yêu cầu bài toán. Phân tích, đưa ra lời giải Giải bài 2 trang 69 SGK Toán 8 – Cánh diều – Bài 4. Tính chất đường phân giác của tam giác. Cho tam giác ABC có đường trung tuyến AM….
Đề bài/câu hỏi:
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).
Hướng dẫn:
Dựa vào tính chất đường phân giác để chứng minh yêu cầu bài toán.
Lời giải:
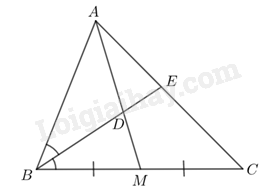
Tam giác ABC có đường phân giác BE nên ta có: \(\frac{{EC}}{{EA}} = \frac{{BC}}{{BA}}\)
Mà M là trung điểm của BC nên \(BC = 2BM\)
\( \Rightarrow \frac{{EC}}{{EA}} = 2\frac{{BM}}{{BA}}\,\,\left( 1 \right)\)
Tam giác ABM có đường phân giác BD nên ta có: \(\frac{{DM}}{{DA}} = \frac{{BM}}{{BA}}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).