Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để tính CH, AH. Hướng dẫn trả lời Giải bài 9.46 trang 63 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 36. Các trường hợp đồng dạng của hai tam giác vuông. Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng \(AB = 6cm\) và \(AC = 8cm\),…
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng \(AB = 6cm\) và \(AC = 8cm\), hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.
Hướng dẫn:
+ Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để tính CH, AH: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Sử dụng kiến thức định lí Pythagore để tính độ dài BC: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải:
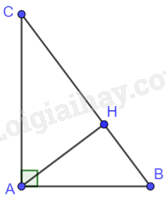
Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) nên \(BC = 10cm\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\).
Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C\) chung. Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$
Suy ra: \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên \(CH = \frac{{C{A^2}}}{{CB}} = \frac{{{8^2}}}{{10}} = \frac{{32}}{5}\left( {cm} \right)\)
Do đó, \(BH = BC – CH = 10 – \frac{{32}}{5} = \frac{{18}}{5}\left( {cm} \right)\)
Vì $\Delta ABC\backsim \Delta HAC\left( cmt \right)$ nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\)
Do đó, \(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = \frac{{24}}{5}\left( {cm} \right)\)