Bài 9.24 trang 56 SBT toán 8 – Kết nối tri thức: Cho hình thang ABCD (AB//CD). Biết rằng AB = 2cm, BD = 4cm, CD = 8cm. Chứng minh rằng BC = 2AD

Đề bài/câu hỏi:

Cho hình thang ABCD (AB//CD). Biết rằng \(AB = 2cm,BD = 4cm,CD = 8cm.\) Chứng minh rằng \(BC = 2AD\)

Hướng dẫn:

Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – góc – cạnh): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

Lời giải:

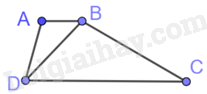
Vì AB//CD nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)

Tam giác ABD và tam giác BDC có:

\(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}}\left( {do\frac{2}{4} = \frac{4}{8}} \right)\), \(\widehat {ABD} = \widehat {BDC}\) (cmt)

Do đó, $\Delta ABD\backsim \Delta BDC\left( c-g-c \right)$

Suy ra: \(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} = \frac{{AD}}{{BC}} = \frac{1}{2}\). Do đó, \(BC = 2AD\)