Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – cạnh – cạnh) để chứng minh hai tam giác đồng dạng. Hướng dẫn giải Giải bài 9.16 trang 55 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 34. Ba trường hợp đồng dạng của hai tam giác. Cho tam giác ABC có các điểm M, N, P lần lượt là trung điểm của BC, CA, AB….
Đề bài/câu hỏi:
Cho tam giác ABC có các điểm M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng $\Delta ABC\backsim \Delta MNP$ và tìm tỉ số đồng dạng.
Hướng dẫn:
Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – cạnh – cạnh) để chứng minh hai tam giác đồng dạng: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải:
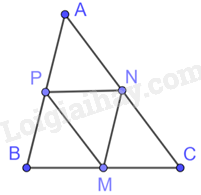
Tam giác ABC có: M, N lần lượt là trung điểm của BC, CA nên MN là đường trung bình của tam giác ABC. Do đó, MN//AB và \(\frac{{AB}}{{MN}} = 2\)
Chứng minh tương tự ta có: \(\frac{{BC}}{{PN}} = 2;\frac{{AC}}{{PM}} = 2\)
Tam giác ABC và tam giác MNP có:
\(\frac{{AB}}{{MN}} = \frac{{BC}}{{PN}} = \frac{{AC}}{{PM}}\left( { = 2} \right)\) nên $\Delta ABC\backsim \Delta MNP$(c.c.c) theo tỉ số đồng dạng là 2.