Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh. Hướng dẫn trả lời Giải bài 3.23 trang 42 sách bài tập toán 8 – Kết nối tri thức với cuộc sống – Bài 14. Hình thoi và hình vuông. Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi….
Đề bài/câu hỏi:
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Hướng dẫn:
Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải:
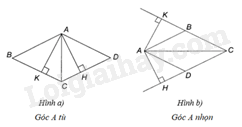
Xét hình bình hành ABCD có đường cao AH (H thuộc đường thẳng CD), và đường cao AK (K thuộc đường thẳng BC) thỏa mãn \(AH = AK\)
Tam giác ACH và tam giác ACK có:
\(\widehat {AHC} = \widehat {AKC} = {90^0}\), \(AH = AK\), cạnh AC chung
Do đó, \(\Delta ACH = \Delta ACK\) (ch – cgv)
Suy ra: \(\widehat {ACK} = \widehat {ACH}\) nên CA là tia phân giác góc BCD.
Hình bình hành ABCD có CA là tia phân giác góc BCD nên ABCD là hình thoi.