Sử dụng kiến thức về áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông. Trả lời Giải bài 7 trang 69 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài 3. Các trường hợp đồng dạng của hai tam giác vuông. Cho tam giác ABC vuông tại A. Tia phân giác của góc A cắt cạnh huyền BC tại M….
Đề bài/câu hỏi:
Cho tam giác ABC vuông tại A. Tia phân giác của góc A cắt cạnh huyền BC tại M. Qua M kẻ đường thẳng vuông góc với BC và cắt AC tại N. Chứng minh rằng:
a) $\Delta MNC\backsim \Delta ABC$.
b) $MN=MB$.
Hướng dẫn:
Sử dụng kiến thức về áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông: Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải:
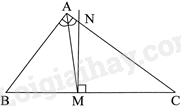
a) Tam giác MNC và tam giác ABC có: $\widehat{NMC}=\widehat{BAC}={{90}^{0}},\widehat{C}\ chung$. Do đó, $\Delta MNC\backsim \Delta ABC\left( g.g \right)$
b) Vì $\Delta MNC\backsim \Delta ABC\left( cmt \right)$ nên $\frac{MN}{AB}=\frac{MC}{AC}\left( 1 \right)$
Vì AM là tia phân giác của góc BAC trong tam giác ABC nên theo tính chất đường phân giác của tam giác ta có: $\frac{MB}{MC}=\frac{AB}{AC}$ hay $\frac{MB}{AB}=\frac{MC}{AC}$ (2)
Từ (1) và (2) ta có: $\frac{MN}{AB}=\frac{MB}{AB}$. Vậy $MN=MB$.