Sử dụng kiến thức diện tích hình vuông: Diện tích hình vuông có độ dài cạnh bằng a là: \(S = {a^2}\. Gợi ý giải Giải bài 7 trang 49 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài tập cuối chương 7. Cho hình vuông ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD,…
Đề bài/câu hỏi:
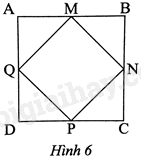
Cho hình vuông ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (Hình 6). Đẳng thức nào sau đây là đúng?
A. \({S_{MNPQ}} = \frac{1}{4}{S_{ABCD}}\).
B. \({S_{MNPQ}} = \frac{1}{3}{S_{ABCD}}\).
C. \({S_{MNPQ}} = {S_{ABCD}}\).
D. \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\).
Hướng dẫn:
+ Sử dụng kiến thức diện tích hình vuông: Diện tích hình vuông có độ dài cạnh bằng a là: \(S = {a^2}\)
+ Sử dụng kiến thức diện tích tam giác vuông: Diện tích tam giác vuông bằng một nửa độ dài hai cạnh hình vuông.
Lời giải:
Gọi độ dài cạnh của hình vuông ABCD bằng a.
Vì ABCD là hình vuông nên \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0},AB = BC = CD = DA = a\)
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên \(AM = MB = BN = NC = PC = PD = QD = QA = \frac{a}{2}\)
Diện tích hình vuông ABCD là: \({S_{ABCD}} = A{B^2} = {a^2}\)
Diện tích tam giác vuông QAM vuông tại A là: \({S_1} = \frac{1}{2}AM.AQ = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông BNM vuông tại B là: \({S_2} = \frac{1}{2}BM.BN = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông PNC vuông tại C là: \({S_3} = \frac{1}{2}CN.PC = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Diện tích tam giác vuông QDP vuông tại D là: \({S_4} = \frac{1}{2}DP.DQ = \frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{8}\)
Do đó, \({S_{MNPQ}} = {S_{ABCD}} – {S_1} – {S_2} – {S_3} – {S_4} = {a^2} – 4.\frac{{{a^2}}}{8} = \frac{{{a^2}}}{2}\)
Suy ra: \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\)
Chọn D.