Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M. Vận dụng kiến thức giải Giải bài 5 trang 60 sách bài tập toán 8 – Chân trời sáng tạo – Bài 3. Hình thang – Hình thang cân. Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M,…
Đề bài/câu hỏi:
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho \(AM = AN.\) Chứng minh tứ giác MNBC là hình thang cân.
Hướng dẫn:
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho \(AM = AN.\) Chứng minh tứ giác MNBC là hình thang cân.
Lời giải:
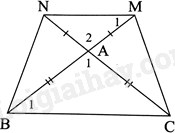
Vì tam giác ABC cân tại A nên \(AB = AC\) và \(\widehat {{B_1}} = \widehat {ACB}\), mà \(\widehat {{B_1}} + \widehat {ACB} + \widehat {{A_1}} = {180^0}\). Do đó, \(\widehat {{B_1}} = \frac{{{{180}^0} – \widehat {{A_1}}}}{2}\) (1)
Vì \(AM = AN\left( {gt} \right)\) nên tam giác AMN cân tại A.
Do đó, \(\widehat {{M_1}} = \widehat {ANM}\), mà \(\widehat {{M_1}} + \widehat {ANM} + \widehat {{A_2}} = {180^0}\)
Do đó, \(\widehat {{M_1}} = \frac{{{{180}^0} – \widehat {{A_2}}}}{2}\) (2)
Lại có: \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc đối đỉnh) (3)
Từ (1), (2), (3) ta có: \(\widehat {{B_1}} = \widehat {{M_1}}\), mà hai góc này ở vị trí so le trong nên MN//BC. Do đó, tứ giác MNBC là hình thang (5).
Ta có: \(AM = AN\left( {gt} \right)\), \(AB = AC\)(cmt) nên \(AM + AB = AN + AC\), suy ra \(BM = CN\) (6)
Từ (5) và (6) ta có: Tứ giác MNBC là hình thang cân.