Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc. Hướng dẫn giải Giải bài 5 trang 57 sách bài tập toán 8 – Chân trời sáng tạo – Bài 2. Tứ giác. Cho tứ giác ABCD có \(\widehat C – \widehat D = {10^0}\)….
Đề bài/câu hỏi:
Cho tứ giác ABCD có \(\widehat C – \widehat D = {10^0}\). Các tia phân giác của góc A và góc B cắt nhau tại I. Biết \(\widehat {AIB} = {65^0}\). Tính góc C và góc D.
Hướng dẫn:
Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc: Tổng số đo các góc của một tứ giác bằng 360 độ.
Lời giải:
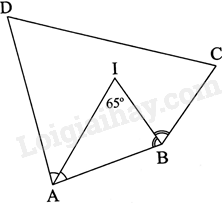
Tam giác AIB có: \(\widehat {AIB} + \widehat {IAB} + \widehat {IBA} = {180^0}\)
Suy ra: \(\widehat {IAB} + \widehat {IBA} = {180^0} – \widehat {AIB} = {115^0}\)
Vì AI là tia phân giác của góc DAB nên \(\widehat {DAB} = 2\widehat {IAB}\)
Vì BI là tia phân giác của góc ABC nên \(\widehat {ABC} = 2\widehat {ABI}\)
Do đó: \(\widehat {ABC} + \widehat {DAB} = 2\left( {\widehat {IAB} + \widehat {IBA}} \right) = {230^0}\)
Tứ giác ABCD có: \(\widehat C + \widehat D = {360^0} – \left( {\widehat {ABC} + \widehat {DAB}} \right) = {130^0}\)
Mà \(\widehat C – \widehat D = {10^0}\) nên \(\widehat C = {10^0} + \widehat D\)
Do đó: \(2\widehat D + {10^0} = {130^0}\), do đó \(\widehat D = {60^0}\), suy ra \(\widehat C = {60^0} + {10^0} = {70^0}\)