Sử dụng kiến thức về định lí Thalès trong tam giác để tính. Lời giải bài tập, câu hỏi Giải bài 5 trang 42 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài 1. Định lí Thalès trong tam giác. Cho tam giác ABC có AM là đường trung tuyến \(\left( {M \in BC} \right)\)….
Đề bài/câu hỏi:
Cho tam giác ABC có AM là đường trung tuyến \(\left( {M \in BC} \right)\). Lấy điểm E thuộc AM sao cho \(AE = 3EM.\) Tia BE cắt AC tại N. Tính tỉ số \(\frac{{AN}}{{NC}}\).
Hướng dẫn:
Sử dụng kiến thức về định lí Thalès trong tam giác để tính: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải:
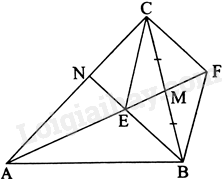
Lấy điểm F trên tia AM sao cho M là trung điểm của EF. Tứ giác ECFB có: M là trung điểm của BC, M là trung điểm của EF nên tứ giác ECFB là hình bình hành. Do đó, CF//BE hay CF//EN.
Trong tam giác ACF có: CF//EN nên theo định lí Thalès trong tam giác ta có: \(\frac{{AN}}{{NC}} = \frac{{AE}}{{EF}} = \frac{3}{2}\)