Sử dụng kiến thức về đường trung bình của tam giác để chứng minh. Trả lời Giải bài 3 trang 45 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài 2. Đường trung bình của tam giác. Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,…
Đề bài/câu hỏi:
Cho tam giác ABC, hai đường trung tuyến BM và CN cắt nhau tại G \(\left( {M \in AC,N \in AB} \right)\). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:
a) MN//DE
b) ND//ME
Hướng dẫn:
+ Sử dụng kiến thức về đường trung bình của tam giác để chứng minh: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Sử dụng kiến thức về tính chất của đường trung bình của tam giác để chứng minh: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải:
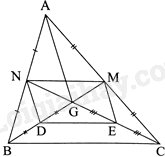
a) Vì BM và CN là các đường trung tuyến của tam giác ABC nên \(AM = MC,AN = NB\)
Tam giác ABC có: \(AM = MC,AN = NB\) nên MN là đường trung bình của tam giác ABC.
Do đó, \(MN//BC,MN = \frac{1}{2}BC\)
Tam giác GBC có: D, E lần lượt là trung điểm của GB, GC nên DE là đường trung bình của tam giác GBC.
Do đó, DE//BC, \(DE = \frac{1}{2}BC\)
Ta có: MN//BC, DE//BC nên MN//DE
b) Tứ giác MNDE có: MN//DE, \(MN = DE\left( { = \frac{{BC}}{2}} \right)\)
Do đó, tứ giác MNDE là hình bình hành. Do đó, ND//ME