Bài 15 (ôn tập chương 7) trang 51 SBT toán 8 – Chân trời sáng tạo tập 2: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Tia phân giác của ∠ ABC cắt AC tại D. a) Tính độ dài DA, DC

Đề bài/câu hỏi:

Cho tam giác ABC vuông tại A có \(AB = 6cm,AC = 8cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.

a) Tính độ dài DA, DC.

b) Tia phân giác của \(\widehat {ACB}\) cắt BD ở I. Gọi M là trung điểm của BC. Chứng minh \(\widehat {BIM} = {90^0}\).

Hướng dẫn:

Sử dụng kiến thức về tính chất của đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.

Lời giải:

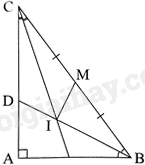
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại A có: \(BC = \sqrt {A{B^2} + A{C^2}} = 10\left( {cm} \right)\)

Vì BD là tia phân giác của góc ABC trong tam giác ABC nên theo tính chất đường phân giác của tam giác ta có: \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\)

Do đó, \(\frac{{DA}}{3} = \frac{{DC}}{5} = \frac{{AC}}{8} = 1\). Suy ra: \(DA = 3cm,DC = 5cm\)

b) Áp dụng định lí Pythagore vào tam giác ABD vuông tại A có: \(BD = \sqrt {A{B^2} + A{D^2}} = 3\sqrt 5 \left( {cm} \right)\)

Vì CI là đường phân giác của góc DCB trong tam giác BCD nên theo tính chất đường phân giác của tam giác ta có: \(\frac{{ID}}{{IB}} = \frac{{DC}}{{BC}} = \frac{5}{{10}} = \frac{1}{2}\), suy ra \(\frac{{ID}}{1} = \frac{{IB}}{2} = \frac{{BD}}{3} = \sqrt 5 \)

Suy ra: \(ID = \sqrt 5 cm,IB = 2\sqrt 5 cm\)

Chứng minh \(\Delta IDC = \Delta IMC\left( {c – g – c} \right)\) nên \(IM = ID = \sqrt 5 cm\)

Vì \(I{M^2} + I{B^2} = 25 = M{B^2}\) nên tam giác IMB vuông tại I (định lí Pythagore đảo). Do đó, \(\widehat {BIM} = {90^0}\)