Sử dụng kiến thức về đường chéo của tứ giác để tìm số đo góc còn lại: Trong tứ giác. Phân tích và giải Giải bài 12 trang 74 sách bài tập toán 8 – Chân trời sáng tạo – Bài tập cuối chương 3. Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\)….
Đề bài/câu hỏi:
Cho tứ giác EKIT có \(EK = ET,IK = IT,\widehat {KET} = {90^0},\widehat {EKI} = {105^0}\). Gọi S là giao điểm của hai đường chéo. Tính số đo các góc \(\widehat {KIS},\widehat {SKI}\)
Hướng dẫn:
Sử dụng kiến thức về đường chéo của tứ giác để tìm số đo góc còn lại: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau
Lời giải:
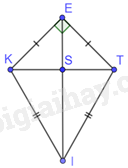
Vì \(EK = ET\) nên E thuộc đường trung trực của KT.
Vì \(IK = IT\) nên I thuộc đường trung trực của KT.
Do đó, EI là đường trung trực của KT. Suy ra: \(EI \bot KT\) tại S.
Tam giác EKT có: \(EK = ET\), \(\widehat {KET} = {90^0}\) nên tam giác EKT vuông cân tại E. Do đó, ES là đường trung trực đồng thời là đường phân giác. Do đó, \(\widehat {KES} = \frac{1}{2}\widehat {KET} = {45^0}\)
Tam giác KEI có: \(\widehat {KIE} = {180^0} – \widehat {EKI} – \widehat {KES} = {30^0}\)
Tam giác KIS vuông tại S có: \(\widehat {SKI} = {90^0} – \widehat {KIS} = {90^0} – {30^0} = {60^0}\)