Sử dụng kiến thức về xác suất thực nghiệm của biến cố. Hướng dẫn trả lời Giải bài 1 trang 91 sách bài tập toán 8 – Chân trời sáng tạo tập 2 – Bài 2. Xác suất lí thuyết và xác suất thực nghiệm. Cho tấm bìa như Hình 1. Thu xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng…
Đề bài/câu hỏi:
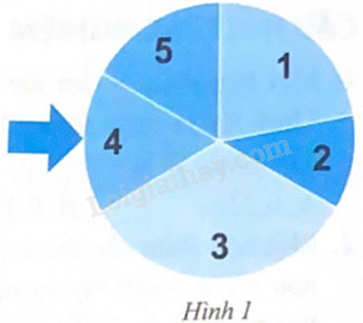
Cho tấm bìa như Hình 1. Thu xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Kết quả sau 150 lần xoay được ghi lại ở bảng sau:
|
Ô số |
1 |
2 |
3 |
4 |
5 |
|
Số lần |
36 |
12 |
54 |
27 |
21 |
Hãy tính xác suất thực nghiệm của các biến cố:
A: “Mũi tên chỉ vào ô ghi số 1”;
B: “Mũi tên chỉ vào ô ghi số chẵn”;
C: “Mũi tên chỉ vào ô ghi số lớn hơn 3”.
Hướng dẫn:
Sử dụng kiến thức về xác suất thực nghiệm của biến cố: Gọi P(A) là xác suất xuất hiện biến cố A khi thực hiện một phép thử. Gọi m(A) là số lần xuất hiện biến cố A khi thực hiện một phép thử đó m lần. Xác suất thực nghiệm của biến cố A là tỉ số \(\frac{{m\left( A \right)}}{m}\).
Lời giải:
Vì có 36 lần xảy ra biến cố A trong 150 lần thử nên xác suất thực nghiệm của các biến cố A sau 150 lần thử là: \(\frac{{36}}{{150}} = 0,24\)
Vì có \(12 + 27 = 39\) lần xảy ra biến cố B trong 150 lần thử nên xác suất thực nghiệm của các biến cố B sau 150 lần thử là: \(\frac{{39}}{{150}} = 0,26\)
Vì có \(27 + 21 = 48\) lần xảy ra biến cố C trong 150 lần thử nên xác suất thực nghiệm của các biến cố C sau 150 lần thử là: \(\frac{{48}}{{150}} = 0,32\)