Áp dụng tính chất đường phân giác của tam giác: trong tam giác. Trả lời Giải bài 23 trang 67 sách bài tập toán 8 – Cánh diều – Bài 4. Tính chất đường phân giác của tam giác. Cho hình bình hành \(ABCD\). Đường phân giác của góc \(A\) cắt \(BD\) tại \(E\),…
Đề bài/câu hỏi:
Cho hình bình hành \(ABCD\). Đường phân giác của góc \(A\) cắt \(BD\) tại \(E\), đường phân giác của góc \(B\) cắt \(AC\) tại \(F\). Chứng minh:
a) \(\frac{{BE}}{{ED}} = \frac{{AF}}{{FC}}\);
b) \(EF//AB\)
Hướng dẫn:
Áp dụng tính chất đường phân giác của tam giác: trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Lời giải:
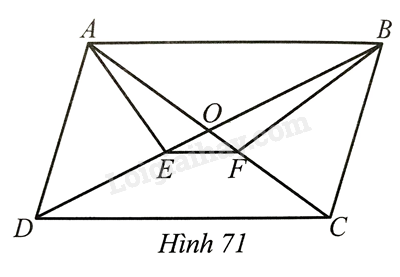
a) Tam giác \(ABD\) có \(AE\) là đường phân giác của góc \(A\) nên \(\frac{{BE}}{{ED}} = \frac{{AB}}{{AD}}\) (1).
Tam giác \(ABC\) có \(BF\) là đường phân giác của góc \(B\) nên \(\frac{{AF}}{{FC}} = \frac{{AB}}{{BC}}\) (2)
Vì \(AD = BC\) nên từ (1) và (2) suy ra \(\frac{{BE}}{{ED}} = \frac{{AF}}{{FC}}\).
b) Ta có: \(\frac{{BE}}{{ED}} = \frac{{AF}}{{FC}}\) suy ra \(\frac{{BE + ED}}{{ED}} = \frac{{AF + FC}}{{FC}}\) hay \(\frac{{BD}}{{ED}} = \frac{{AC}}{{FC}}\) hay \(\frac{{2OD}}{{ED}} = \frac{{2OC}}{{FC}}\), suy ra \(\frac{{OD}}{{ED}} = \frac{{OC}}{{FC}}\). Do đó \(EF//CD\) hay \(EF//AB\).