Áp dụng công thức \({S_{xq}} = \frac{1}{2}. C. d\), trong đó \({S_{xq}}\) là diện tích xung quanh, \(C\) là chu vi đáy, \(d\. Lời giải Giải bài 22 trang 79 sách bài tập toán 8 – Cánh diều – Bài tập cuối Chương 4. Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b:…
Đề bài/câu hỏi:
Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b:
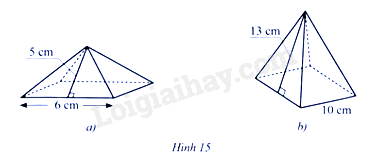
Hướng dẫn:
Áp dụng công thức \({S_{xq}} = \frac{1}{2}.C.d\), trong đó \({S_{xq}}\) là diện tích xung quanh, \(C\) là chu vi đáy, \(d\) là độ dài trung đoạn của hình chóp tứ giác đều.
Lời giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều \({S_{xq}} = \frac{1}{2}.C.d\), ta có:
Diện tích xung quanh của hình chóp tứ giác đều ở hình 15a là:
\(\frac{1}{2}.\left( {6.4} \right).5 = 60\left( {c{m^2}} \right)\)
Diện tích xung quanh của hình chóp tứ giác đều ở hình 15b là:
\(\frac{1}{2}.\left( {10.4} \right).13 = 260\left( {c{m^2}} \right)\)