Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó. Hướng dẫn giải Giải bài 11 trang 62 sách bài tập toán 8 – Cánh diều – Bài 2. Ứng dụng của định lí Thalès trong tam giác. Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay \(A,B,C\…
Đề bài/câu hỏi:
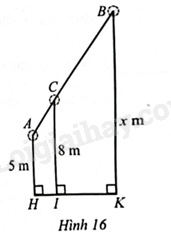
Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay \(A,B,C\) của băng chuyền đặt cách mặt đất ở các độ cao lần lượt là \(AH = 5\) (m), \(CI = 8\) (m), \(BK = x\) (m) (Hình 16).
Tính \(x\), biết \(AC = \frac{2}{5}CB\)
Hướng dẫn:
Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải:
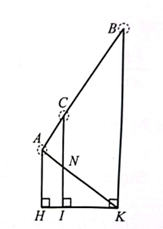
Do \(AC = \frac{2}{5}CB\) nên \(AC = \frac{2}{7}AB\). Gọi \(N\) là giao điểm của \(AK\) và \(CI\). Do \(CN//BK\) nên theo hệ quả của định lí Thales, ta có: \(\frac{{AC}}{{AB}} = \frac{{CN}}{{BK}}\) hay \(\frac{{CN}}{x} = \frac{2}{7}\). Suy ra \(CN = \frac{2}{7}x\) (1). Tương tự, do \(IN//AH,CN//BK\) nên \(\frac{{IN}}{{AH}} = \frac{{IK}}{{KH}} = \frac{{BK}}{{KA}} = \frac{{CB}}{{BA}} = \frac{5}{7}\) hay \(\frac{{IN}}{5} = \frac{5}{7}\). Suy ra \(IN = 5.\frac{5}{7} = \frac{{25}}{7}\) (m) (2).
Từ (1) và (2) ta có: \(CI = CN + IN = \frac{2}{7}x + \frac{{25}}{7}\).
Lại có \(CI = 8\) (m) nên \(\frac{2}{7}x + \frac{{25}}{7} = 8\). Vậy \(x = 15,5\).