Đề cương ôn tập học kì 2 Toán 8 – Chân trời sáng tạo: A. NỘI DUNG ÔN TẬP Đại số Phương trình – Phương trình bậc nhất một ẩn – Giải bài toán bằng cách lập phương trình bậc nhất một ẩn Hình

A. NỘI DUNG ÔN TẬP

Đại số

Phương trình

– Phương trình bậc nhất một ẩn

– Giải bài toán bằng cách lập phương trình bậc nhất một ẩn

Hình học

Hình đồng dạng

– Hai tam giác đồng dạng

– Các trường hợp đồng dạng của hai tam giác

– Các trường hợp đồng dạng của hai tam giác vuông

– Hai hình đồng dạng

Xác suất

Một số yếu tố xác suất

– Mô tả xác suất bằng tỉ số

– Xác suất lí thuyết và xác suất thực nghiệm

B. BÀI TẬP

Đề bài/câu hỏi:

I. Phần trắc nghiệm

Câu 1: Trong các phương trình sau, đâu là phương trình bậc nhất một ẩn

A. \(3x – y = 0\).

B. \(2y + 1 = 0\).

C. \(4 + 0.x = 0\).

D. \(3{x^2} = 0\).

Câu 2: Phương trình bậc nhất một ẩn \(ax + b = 0\) với hệ số b = 3 là phương trình nào

A. \(3x + 1 = 0\).

B. \(x – 3 = 0\).

C. \( – x + 3 = 0\).

D. \(3x – 3 = 0\).

Câu 3: Phương trình \(6x – 3 = 0\) có nghiệm là

A. \(x = 2\).

B. \(x = – \frac{1}{2}\).

C. \(x = – 2\).

D. \(x = \frac{1}{2}\).

Câu 4: Đưa phương trình \(2\left( {x + 2} \right) = 1 – 2x\) về dạng \(ax + b = 0\), ta được:

A. \(4x + 3 = 0\).

B. \( – 2x + 1 = 0\).

C. \(4x + 5 = 0\).

D. \(2x + 4 = 0\).

Câu 5: Tập nghiệm S của phương trình \(3\left( {x + 1} \right) + 2x = 7 + \left( {x – 2} \right)\) là:

A. \(S = \left\{ 0 \right\}\).

B. \(S = \left\{ {\frac{1}{2}} \right\}\).

C. \(S = \emptyset \).

D. \(S = \mathbb{R}\).

Câu 6: Phương trình \(2x + m – x + 4 = 0\) nhận \(x = – 3\) thì m là:

A. \(m = 1\).

B. \(m = 2\).

C. \(m = – 1\).

D. \(m = – 2\).

Câu 7: Chọn câu sai trong các câu sau:

A. Gọi số học sinh của một lớp là x (học sinh thì điều kiện là \(x \in N*\).

B. Gọi thời gian làm của một xưởng là x (ngày) thì điều kiện là \(x > 0\).

C. Gọi số bài tập của một học sinh làm trong một ngày là x thì điều kiện là \(x < 0\).

D. Gọi tốc độ của một xe ô tô là x thì điều kiện của x là \(x > 0\).

Câu 8: Xe máy đi từ A đến B với vận tốc \(x\left( {km/h} \right)\). Ô tô đi từ B về A với vận tốc nhanh hơn vận tốc của xe máy là \(15km/h\). Vậy vận tốc của ô tô được biểu diễn theo x là:

A. \(x – 15\left( {km/h} \right)\).

B. \(15x\left( {km/h} \right)\).

C. \(15 – x\left( {km/h} \right)\).

D. \(x + 15\left( {km/h} \right)\).

Câu 9: Trên một khúc sông, một chiếc thuyền chạy với vận tốc tối đa đang di chuyển xuôi dòng, một người đứng trên bờ đo được vận tốc của chiếc thuyền là 35km/h. Biết vận tốc dòng nước là 5km/h. Hỏi nếu thuyền đó chạy ngược dòng với vận tốc tối đa thì người đứng trên bờ đo được vận tốc của thuyền lúc đó là bao nhiêu?

A. 30km/h.

B. 35km/h.

C. 40km/h.

D. 70km/h.

Câu 10: Cho $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k. Vậy k bằng tỉ số nào sau đây?

A. \(k = \frac{{AB}}{{BC}}\).

B. \(k = \frac{{AC}}{{DF}}\).

C. \(k = \frac{{DE}}{{AB}}\).

D. \(k = \frac{{DE}}{{DF}}\).

Câu 11: Cho hình vẽ sau, biết DE // BC và các kích thước như hình vẽ. Độ dài đoạn AE là

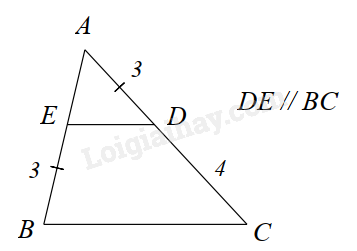
A. \(AE = \frac{3}{4}\).

B. \(AE = \frac{4}{3}\).

C. \(AE = \frac{4}{9}\).

D. \(AE = \frac{9}{4}\).

Câu 12: Cho tam giác ABC cân tại A có AB = 15cm, BC = 10cm, đường phân giác của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là:

A. 3cm.

B. 6cm.

C. 9cm.

D. 12cm.

Câu 13: Tam giác ABC có HK là đường trung bình \(\left( {H \in AC,K \in BC} \right)\). Khi đó $\Delta ABC\backsim \Delta HKC$ theo tỉ số k bằng bao nhiêu?

A. \(k = 2\).

B. \(k = \frac{1}{2}\).

C. \(k = 1\).

D. \(k = 0\).

Câu 14: Cho hình vẽ sau, biết \(\Delta ABC,\Delta ADE\) là tam giác cân.

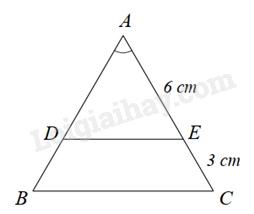
Khẳng định nào sau đây là đúng:

A. $\Delta ADE\backsim \Delta ABC\left( g.g \right)$ với $k=2$.

B. $\Delta ADE\backsim \Delta ABC\left( c.c.c \right)$ với $k=\frac{2}{3}$.

C. $\Delta ABC\backsim \Delta ADE\left( c.g.c \right)$ với $k=\frac{3}{2}$.

D. $\Delta ABC\backsim \Delta ADE\left( g.g \right)$ với $k=\frac{1}{2}$.

Câu 15: Cho $\Delta ABC\backsim \Delta DEF$. AM, DN lần lượt là hai tia phân giác của \(\widehat A,\widehat D\). Khi đó $\Delta ABM\backsim \Delta DEN$ theo trường hợp nào?

A. góc – góc.

B. cạnh – góc – cạnh.

C. cạnh – cạnh – cạnh.

D. cạnh huyền – góc nhọn.

Câu 16: Cho $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng k = 2. Khi đó chu vi \(\Delta ABC\) gấp mấy lần chu vi \(\Delta DEF\)?

A. 1.

B. 2.

C. 4.

D. 8.

Câu 17: Cho tam giác ABC có M, N lần lượt nằm trên cạnh AB, AC sao cho MN // BC. Biết AM = 16cm, AN = 20cm, NC = 15cm. Khi đó độ dài AB bằng:

A. 28cm.

B. 26cm.

C. 24cm.

D. 22cm.

Câu 18: Cho hình thang ABCD (AB // CD), có hai đường chéo AC và BD cắt nhau tại I. Biết AB = 16cm, CD = 40cm. Khi đó $\Delta AIB\backsim \Delta CID$ với tỉ số:

A. \(k = \frac{2}{3}\).

B. \(k = \frac{3}{2}\).

C. \(k = \frac{2}{5}\).

D. \(k = \frac{5}{2}\).

Câu 19: Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4cm , 8cm và 10cm Tam giác thứ hai có chu vi là 33cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?

A. 6cm, 12cm, 15cm.

B. 8cm, 16cm, 20cm.

C. 6cm, 9cm, 18cm.

D. 8cm, 10cm, 15cm.

Câu 20: $\Delta ABC\backsim \Delta A’B’C’$ theo tỉ số đồng dạng k = 3 thì tỉ số chiều cao h của \(\Delta ABC\) với chiều cao h’ của \(\Delta A’B’C’\) là:

A. \(\frac{h}{{h’}} = \frac{1}{3}\).

B. \(\frac{h}{{h’}} = 6\).

C. \(\frac{h}{{h’}} = – 3\).

D. \(\frac{h}{{h’}} = 3\).

Câu 21: Cho hình vẽ, $\Delta ABC\backsim \Delta DEC$ theo trường hợp nào?

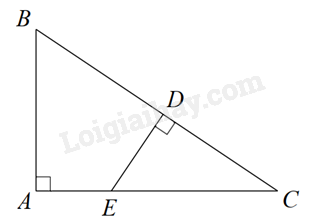
A. Góc – góc.

B. Cạnh – góc – cạnh.

C. Góc – cạnh.

D. Cạnh – cạnh – cạnh.

Câu 22: Cho \(\Delta ABC\) vuông tại A \(\left( {AB \ne AC} \right)\) và \(\Delta DEF\) vuông tại D \(\left( {DE \ne DF} \right)\). Điều nào dưới đây không suy ra $\Delta ABC\backsim \Delta DEF$

A. \(\widehat B = \widehat E\).

B. \(\widehat C = \widehat F\).

C. \(\widehat B + \widehat C = \widehat E + \widehat F\).

D. \(\widehat B – \widehat C = \widehat E – \widehat F\).

Câu 23: Giá trị của x bằng bao nhiêu để hai tam giác đồng dạng

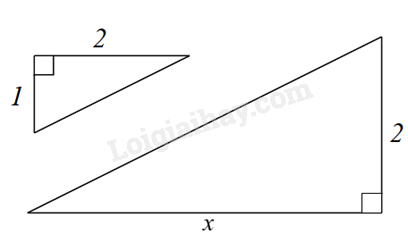
A. \(x = 2\).

B. \(x = \sqrt 3 \).

C. \(x = 4\).

D. \(x = 2\sqrt 3 \).

Câu 24: Cho hình vẽ sau. Biết AB = 3, AC = 4, BC = 5. Khi đó AH là

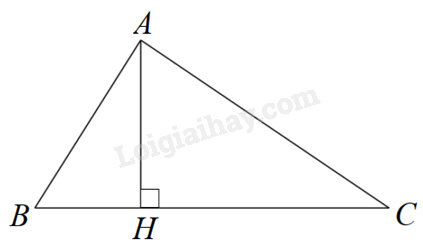
A. \(AH = \frac{{20}}{3}\).

B. \(AH = \frac{{12}}{5}\).

C. \(AH = 2\).

D. \(AH = 6\).

Câu 25: Cho hình vẽ sau. Biết AC // HK. Tỉ số \(\frac{{{S_{\Delta ABC}}}}{{{S_{\Delta HIK}}}}\) bằng:

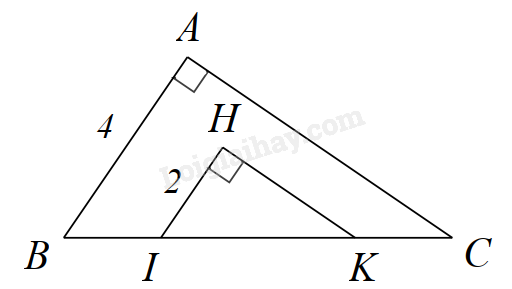
A. 2.

B. 4.

C. \(\frac{1}{2}\).

D. \(\frac{1}{4}\).

Câu 26: Trong các cặp hình sau, hình nào là hình đồng dạng:

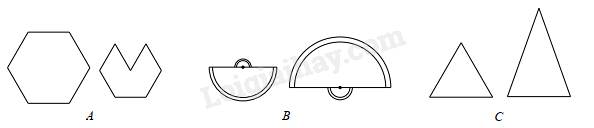
A. Hình A.

B. Hình B.

C. Hình C.

D. Không có hình nào.

Câu 27: Hình A đồng dạng phối cảnh với hình B theo tỉ số đồng dạng là \(k = \frac{2}{3}\) thì hình B đồng dạng phối cảnh với hình A theo tỉ số đồng dạng là bao nhiêu?

A. \(\frac{1}{2}\).

B. \(\frac{2}{3}\).

C. \(\frac{1}{3}\).

D. \(\frac{3}{2}\).

Câu 28: Cho hình 1 đồng dạng phối cảnh với hình 2 với tỉ số đồng dạng là 2.

Khi đó tỉ số nào sau đây đúng?

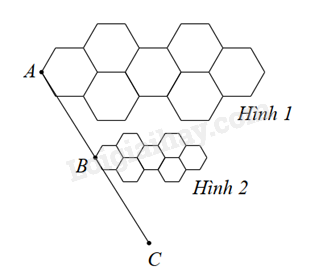
A. \(\frac{{AB}}{{BC}} = 2\).

B. \(\frac{{AB}}{{AC}} = 2\).

C. \(\frac{{AC}}{{AB}} = 2\).

D. \(\frac{{BC}}{{BA}} = 2\).

Câu 29: Cho hình bên, biết \(M \in AH\) thỏa mãn \(AM = 2MH\) và \(MN//BC\). Chọn câu đúng trong các câu sau:

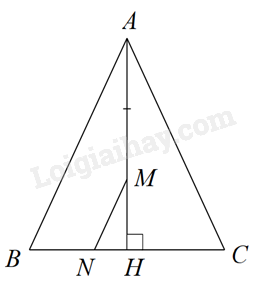
A. \(\Delta HMN\) đồng dạng phối cảnh với \(\Delta HAC\), tâm phối cảnh H.

B. \(\Delta HMN\) đồng dạng phối cảnh với \(\Delta HAB\), tâm phối cảnh H.

C. \(\Delta HAB\) đồng dạng phối cảnh với \(\Delta HAC\), tâm phối cảnh H.

D. Cả ba câu trên đều đúng.

Câu 30: Một hộp chứa 15 tấm thẻ cùng loại được đánh số từ 11 đến 25. Minh lấy ngẫu nhiên một thẻ từ hộp. Xác suất để thẻ chọn ra ghi số chia hết cho 3 là:

A. \(\frac{1}{2}\).

B. \(\frac{1}{3}\).

C. \(\frac{1}{4}\).

D. \(\frac{1}{5}\).

Câu 31: Một hộp chứa thẻ màu xanh và thẻ màu đỏ có kích thước và khối lượng như nhau. Hải lấy ra ngẫu nhiên một thẻ từ hộp, xem màu rồi trả lại hộp. Lặp lại thí nghiệm đó 50 lần, Hải thấy có 14 lần lấy được thẻ màu xanh. Xác suất thực nghiệm của biến cố “Lấy được thẻ màu đỏ” là:

A. 0,14.

B. 0,28.

C. 0,72.

D. 0,86.

Câu 32: Tỉ lệ học sinh bị cận thị ở một trường trung học cơ sở là 18%. Gặp ngẫu nhiên một học sinh ở trường, xác suất học sinh đó bị cận thị là:

A. 0,18.

B. 0,82.

C. 0,92.

D. 0,5.

Câu 33: An gieo 3 con xúc sắc cân đối và đồng chất. Xác suất của biến cố “Tích số chấm xuất hiện trên ba con xúc xắc bằng 28” là:

A. 0.

B. \(\frac{1}{{18}}\).

C. \(\frac{1}{{36}}\).

D. \(\frac{1}{{12}}\).

Câu 34: Lớp 8A có 38 học sinh, trong đó có 18 bạn nữ. Có 8 bạn nữ tham gia câu lạc bộ thể thao và 10 bạn nam không tham gia câu lạc bộ thể thao. Chọn ngẫu nhiên một học sinh trong lớp, xác suất để học sinh đó là một bạn nam tham gia câu lạc bộ thể thao là

A. \(\frac{{10}}{{20}}\).

B. \(\frac{5}{{19}}\).

C. \(\frac{{18}}{{21}}\).

D. \(\frac{9}{{23}}\).

Câu 35: Một túi đựng các quả cầu giống hệt nhau, chỉ khác màu, trong đó có 27 quả màu đỏ, 35 quả màu tím, 7 quả màu vàng, 11 quả màu trắng và 15 quả màu đen. Lấy ngẫu nhiên 1 quả trong túi. Xác suất lấy được quả cầu màu tím là:

A. \(\frac{{33}}{{95}}\).

B. \(\frac{{34}}{{95}}\).

C. \(\frac{7}{{19}}\).

D. \(\frac{{19}}{{35}}\).

II. Phần tự luận

Bài 1. Giải các phương trình sau:

a) \(7x – 4 = 0\)

b) \(9 – 5x = 0\)

c) \(11x – \left( {3x + 3} \right) = 8\left( {x – 2} \right)\)

d) \(\frac{{2x – 1}}{5} + x = 3 + \frac{{3 – x}}{4}\)

Bài 2. Tìm m để phương trình \(\left( {m – 1} \right)x = {m^2} – 1\)

a) Vô nghiệm.

b) Vô số nghiệm.

c) Có nghiệm duy nhất.

Bài 3. Bác An đầu tư 500 triệu đồng vào hai tài khoản: mua trái phiếu doanh nghiệp với lãi suất 8% một năm và gửi tiết kiệm ngân hàng với lãi suất 6% một năm. Cuối năm bác An nhận được 34 triệu đồng tiền lãi. Hỏi bác An đã đầu tư vào mỗi tài khoản bao nhiêu tiền?

Bài 4. Một xe tải đi từ M đến N với tốc độ 50 km/h. Khi từ N quay về M xe chạy với tốc độ 40 km/h. Thời gian cả đi lẫn về mất 5 giờ 24 phút không kể thời gian nghỉ. Tính chiều dài quãng đường MN.

Bài 5. Hai công ty viễn thông đưa ra hai gói cước cho điện thoại cố định như sau:

a) Gọi x là số phút gọi trong tháng. Hãy biểu thị theo x, số tiền phải trả trong thẳng (tính theo nghìn đồng) khi sử dụng mỗi gói cước nói trên.

b) Hỏi với bao nhiêu phút gọi thì số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau?

Bài 6. Cho \(\Delta KBC\) vuông tại K có KB < KC. Tia phân giác của \(\widehat B\) cắt KC tại H . Qua C vẽ đường thẳng vuông góc với tia BH tại I .

a) Chứng minh $\Delta BHK\backsim \Delta CHI$.

b) Chứng minh \(C{I^2} = IH.IB\).

c) Tia BK cắt CI tại A, tia AH cắt BC tại D .

Chứng minh KC là phân giác của \(\widehat {IKD}\).

Bài 7. Cho ΔABC vuông tại A, biết \(AB = 3cm,BC = 5cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.

a) Vẽ tia Cx vuông góc với BD tại E và tia Cx cắt đường thẳng AB tại F.

Chứng minh $\Delta ABD\backsim \Delta EBC$.

b) Tia FD cắt BC tại H. Kẻ đường thẳng qua H và vuông góc với AB tại M.

Chứng minh \(MH.AB = FH.MB\).

Bài 8. Cho ΔABC vuông tại A có AB < AC , đường cao AH .

a) Chứng minh $\Delta HAC\backsim \Delta ABC$

b) Chứng minh \(H{A^2} = HB.HC\)

c) Gọi D và E lần lượt là trung điểm của AB, BC.

Chứng minh \(CH.CB = 4.D{E^2}\)

d) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và đường thẳng DE . Gọi N là giao điểm của AH và CM . Chứng minh N là trung điểm của AH.

Bài 9. Một hộp chứa 6 tấm thẻ cùng loại được đánh số lần lượt là 2; 3; 5; 8; 13; 21. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố:

A: ‘‘Số ghi trên thẻ là số lẻ’’.

B: ‘‘Số ghi trên thẻ là số nguyên tố’’.

C: ‘‘Số ghi trên thẻ là số chính phương’’.

Bài 10. Khuê tung hai đồng xu giống nhau 100 lần và ghi lại kết quả ở bảng sau:

Tính xác suất thực nghiệm của biến cố : ‘‘Hai đồng xu đều xuất hiện mặt sấp sau 100 lần tung’’.

Bài 11*. Giải phương trình \(\left( {3x – 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = – 16\)

Bài 12*. Cho các số thực a, b, c thỏa mãn abc = 2024. Tính giá trị của biểu thức:

\(P = \frac{{2bc – 2024}}{{3c – 2bc + 2024}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{4048 – 3ac}}{{3ac – 4048 + 2024a}}\)

Bài 13*. Cho 2024 số: \({a_1},{a_2},…,{a_{2024}}\) với \({a_k} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}}\) \(\left( {k = 1,2,…,2024} \right)\).

Tính giá trị biểu thức \(A = {a_1} + {a_2} + … + {a_{2024}}\).

——– Hết ——–

Lời giải:

I. Phần trắc nghiệm

II. Phần tự luận

Bài 1. Giải các phương trình sau:

a) \(7x – 4 = 0\)

b) \(9 – 5x = 0\)

c) \(11x – \left( {3x + 3} \right) = 8\left( {x – 2} \right)\)

d) \(\frac{{2x – 1}}{5} + x = 3 + \frac{{3 – x}}{4}\)

Hướng dẫn:

Đưa phương trình về dạng ax + b = 0 để giải.

Lời giải

a) \(7x – 4 = 0\)

\(\begin{array}{l}7x = 4\\x = \frac{4}{7}\end{array}\)

Vậy \(x = \frac{4}{7}\).

b) \(9 – 5x = 0\)

\(\begin{array}{l}5x = 9\\x = \frac{9}{5}\end{array}\)

Vậy \(x = \frac{9}{5}\).

c) \(11x – \left( {3x + 3} \right) = 8\left( {x – 2} \right)\)

\(\begin{array}{l}11x – 3x – 3 = 8x – 16\\8x – 8x = – 16 + 3\end{array}\)

\(0x = – 13\) (vô lý)

Vậy phương trình vô nghiệm.

d) \(\frac{{2x – 1}}{5} + x = 3 + \frac{{3 – x}}{4}\)

\(\begin{array}{l}\frac{{4\left( {2x – 1} \right)}}{{20}} + \frac{{20x}}{{20}} = \frac{{3.20}}{{20}} + \frac{{5\left( {3 – x} \right)}}{{20}}\\4\left( {2x – 1} \right) + 20x = 60 + 5\left( {3 – x} \right)\\8x – 4 + 20x = 60 + 15 – 5x\\8x + 20x + 5x = 75 + 4\\33x = 79\\x = \frac{{79}}{{33}}\end{array}\)

Vậy \(x = \frac{{79}}{{33}}\).

Bài 2. Tìm m để phương trình \(\left( {m – 1} \right)x = {m^2} – 1\)

a) Vô nghiệm.

b) Vô số nghiệm.

c) Có nghiệm duy nhất.

Hướng dẫn:

Với phương trình có dạng ax = b.

+ Nếu a = 0 và b = 0 thì phương trình vô số nghiệm.

+ Nếu a = 0 và b \( \ne \) 0 thì phương trình vô nghiệm.

+ Nếu a \( \ne \) 0 thì phương trình có nghiệm duy nhất \(x = \frac{b}{a}\).

Lời giải

a) Để phương trình vô nghiệm thì \(\left\{ \begin{array}{l}m – 1 = 0\\{m^2} – 1 \ne 0\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}m = 1\\m \ne 1\\m \ne – 1\end{array} \right.\).

Vậy không có giá trị nào của m để phương trình vô nghiệm.

b) Để phương trình vô số nghiệm thì \(\left\{ \begin{array}{l}m – 1 = 0\\{m^2} – 1 \ne 0\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}m = 1\\\left[ \begin{array}{l}m = 1\\m = – 1\end{array} \right.\end{array} \right.\) hay \(m = 1\).

Vậy khi m = 1 thì phương trình vô số nghiệm.

c) Để phương trình có nghiệm duy nhất thì \(m – 1 \ne 0\) suy ra \(m \ne 1\).

Khi đó nghiệm của phương trình là \(x = \frac{{{m^2} – 1}}{{m – 1}} = \frac{{\left( {m – 1} \right)\left( {m + 1} \right)}}{{m – 1}} = m + 1\).

Vậy khi \(m \ne 1\) thì phương trình có nghiệm duy nhất \(x = m + 1\).

Bài 3. Bác An đầu tư 500 triệu đồng vào hai tài khoản: mua trái phiếu doanh nghiệp với lãi suất 8% một năm và gửi tiết kiệm ngân hàng với lãi suất 6% một năm. Cuối năm bác An nhận được 34 triệu đồng tiền lãi. Hỏi bác An đã đầu tư vào mỗi tài khoản bao nhiêu tiền?

Hướng dẫn:

Gọi số tiền bác An đầu tư mua trái phiếu doanh nghiệp là x (triệu đồng).

Biểu diễn số tiền bác An đầu tư gửi tiết kiệm ngân hàng, số tiền lãi bác nhận được để lập phương trình.

Giải phương trình ta tìm được số tiền bác đầu tư vào mỗi tài khoản.

Lời giải

Gọi số tiền bác An đầu tư mua trái phiếu doanh nghiệp là x (triệu đồng) (ĐK: \(0 < x < 500\)).

Số tiền bác An đầu tư gửi tiết kiệm ngân hàng là: 500 – x (triệu đồng)

Số tiền lãi bác nhận được từ mua trái phiếu doanh nghiệp là:

\(x.8\% = 0,08x\) (triệu đồng)

Số tiền lãi bác nhận được từ ngân hàng là:

\(\left( {500 – x} \right).6\% = \left( {500 – x} \right).0,06 = 30 – 0,06x\) (triệu đồng)

Theo đề bài, ta có phương trình:

\(\begin{array}{l}0,08x + 30 – 0,06x = 34\\0,02x = 4\\x = 200\left( {TM} \right)\end{array}\)

Vậy số tiền bác An đầu tư mua trái phiếu doanh nghiệp là 200 triệu đồng.

Số tiền bác An đầu tư gửi tiết kiệm ngân hàng là 500 – 200 = 300 triệu đồng.

Bài 4. Một xe tải đi từ M đến N với tốc độ 50 km/h. Khi từ N quay về M xe chạy với tốc độ 40 km/h. Thời gian cả đi lẫn về mất 5 giờ 24 phút không kể thời gian nghỉ. Tính chiều dài quãng đường MN.

Hướng dẫn:

Gọi quãng đường MN là x (km) (x > 0)

Biểu diễn thời gian đi, về theo x và lập phương trình.

Giải phương trình và kiểm tra nghiệm.

Lời giải

Đổi 5 giờ 24 phút = \(\frac{{27}}{5}\) giờ.

Gọi quãng đường MN là x (km) (x > 0)

Vì xe tải đi từ M đến N với vận tốc 50km/h nên ta có thời gian xe tải đi từ M đến N là: \(\frac{x}{{50}}\) (h)

Vì xe tải đi từ N quay về M với vận tốc 40km/h nên ta có thời gian xe tải đi từ N về M là: \(\frac{x}{{40}}\) (h)

Vì thời gian cả đi lẫn về mất 5 giờ 24 phút nên ta có phương trình:

\(\frac{x}{{50}} + \frac{x}{{40}} = \frac{{27}}{5}\)

Giải phương trình ta được x = 120 (TM)

Vậy chiều dài quãng đường MN là 120km.

Bài 5. Hai công ty viễn thông đưa ra hai gói cước cho điện thoại cố định như sau:

a) Gọi x là số phút gọi trong tháng. Hãy biểu thị theo x, số tiền phải trả trong thẳng (tính theo nghìn đồng) khi sử dụng mỗi gói cước nói trên.

b) Hỏi với bao nhiêu phút gọi thì số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau?

Hướng dẫn:

a) Viết biểu thức biểu thị số tiền dựa vào thông tin trong bảng.

b) Lập phương trình biểu thị số tiền phải trả bằng nhau.

Giải phương trình.

Lời giải

a) Số tiền phải trả trong tháng khi sử dụng mỗi gói cước công ty A là:

800x + 33000 (đồng)

Số tiền phải trả trong tháng khi sử dụng mỗi gói cước công ty B là:

600x + 39000 (đồng)

b) Theo đề bài, ta có phương trình: 800x + 33000 = 600x + 39000

Giải phương trình: 800x + 33000 = 600x + 39000

800x – 600x = 39000 – 33000

200x = 6000

x = 30

Vậy với 30 phút gọi thì số tiền phải trả trong tháng khi sử dụng dịch vụ của hai công ty viễn thông này là như nhau.

Bài 6. Cho \(\Delta KBC\) vuông tại K có KB < KC. Tia phân giác của \(\widehat B\) cắt KC tại H . Qua C vẽ đường thẳng vuông góc với tia BH tại I .

a) Chứng minh $\Delta BHK\backsim \Delta CHI$.

b) Chứng minh \(C{I^2} = IH.IB\).

c) Tia BK cắt CI tại A, tia AH cắt BC tại D .

Chứng minh KC là phân giác của \(\widehat {IKD}\).

Hướng dẫn:

a) Chứng minh $\Delta BHK\backsim \Delta CHI$ (g.g)

b) Chỉ ra \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}}\).

Chứng minh $\Delta IHC\backsim \Delta ICB$ (g.g)

Suy ra \(\frac{{IH}}{{IC}} = \frac{{IC}}{{IB}} \Rightarrow I{C^2} = IH.IB\).

c) Chứng minh:

\(\Delta AIB\backsim \Delta AKC\Rightarrow \frac{AI}{AB}=\frac{AK}{AC}\)

\(\Delta AIK\backsim \Delta ABC\Rightarrow \widehat{{{K}_{3}}}=\widehat{ACB}\)

\(\Delta BKD\backsim \Delta BCA\Rightarrow \widehat{{{K}_{4}}}=\widehat{ACB}\)

Suy ra \(\widehat {{K_3}} = \widehat {{K_4}}\).

Mà \(\widehat {{K_3}} + \widehat {{K_2}} = \widehat {{K_4}} + \widehat {{K_1}}\left( { = {{90}^0}} \right)\)

\( \Rightarrow \widehat {{K_1}} = \widehat {{K_2}}\) hay KC là phân giác của \(\widehat {IKD}\).

Lời giải

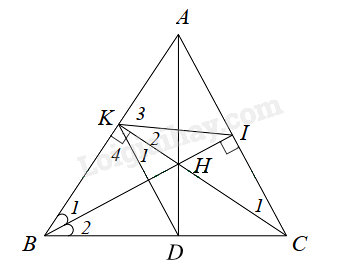
a) Xét \(\Delta BHK\) và \(\Delta CHI\) có:

\(\widehat {BKH} = \widehat {CIH} = {90^0}\)

\(\widehat {KHB} = \widehat {IHC}\) (hai góc đối đỉnh)

Suy ra $\Delta BHK\backsim \Delta CHI$(g.g) (đpcm)

b) Ta có: $\Delta BHK\backsim \Delta CHI$ (cmt) nên \(\widehat {{B_1}} = \widehat {{C_1}}\)

Mà BI là tia phân giác của góc KBC nên \(\widehat {{B_1}} = \widehat {{B_2}}\).

Do đó \(\widehat {{B_2}} = \widehat {{C_1}}\).

Xét \(\Delta IHC\) và \(\Delta ICB\) có:

\(\widehat I\) chung

\(\widehat {{B_2}} = \widehat {{C_1}}\)(cmt)

Suy ra $\Delta IHC\backsim \Delta ICB$ (g.g)

Suy ra \(\frac{{IH}}{{IC}} = \frac{{IC}}{{IB}} \Rightarrow I{C^2} = IH.IB\) (đpcm).

c) Xét \(\Delta AIB\) và \(\Delta AKC\) có:

\(\widehat A\) chung

\(\widehat {{B_1}} = \widehat {{C_1}}\) (cmt)

Suy ra \(\Delta AIB\backsim \Delta AKC\Rightarrow \frac{AI}{AK}=\frac{AB}{AC}\Rightarrow \frac{AI}{AB}=\frac{AK}{AC}\)

Xét \(\Delta AIK\) và \(\Delta ABC\) có:

\(\widehat A\) chung

\(\frac{{AI}}{{AB}} = \frac{{AK}}{{AC}}\)(cmt)

Suy ra \(\Delta AIK\backsim \Delta ABC(c.g.c)\Rightarrow \widehat{{{K}_{3}}}=\widehat{ACB}\) (hai góc tương ứng) (1)

Theo giả thiết, ta có: \(CK \bot AB,BI \bot AC\) nên CK và BI là hai đường cao của tam giác ABC.

Mà BI và CK cắt nhau tại H nên H là giao điểm của 3 đường cao trong tam giác ABC.

Suy ra \(AH \bot BC\) hay \(\widehat {ADB} = {90^o}\)

Xét \(\Delta ABD\) và \(\Delta CBK\) có:

\(\widehat {ADB} = \widehat {CKB} = {90^0}\)

\(\widehat B\) chung

Suy ra $\Delta ABD\backsim \Delta CBK$ (g.g) \( \Rightarrow \frac{{CB}}{{AB}} = \frac{{BK}}{{BD}} \Rightarrow \frac{{BK}}{{CB}} = \frac{{BD}}{{AB}}\)

Xét \(\Delta BKD\) và \(\Delta BCA\) có:

\(\widehat B\) chung

\(\frac{{BK}}{{CB}} = \frac{{BD}}{{AB}}\)

Suy ra \(\Delta BKD\backsim \Delta BCA(c.g.c)\Rightarrow \widehat{{{K}_{4}}}=\widehat{ACB}\) (hai góc tương ứng) (2)

Từ (1) và (2) suy ra \(\widehat {{K_3}} = \widehat {{K_4}}\).

Mà \(\widehat {{K_3}} + \widehat {{K_2}} = \widehat {{K_4}} + \widehat {{K_1}}\left( { = {{90}^0}} \right)\)

\( \Rightarrow \widehat {{K_1}} = \widehat {{K_2}}\) hay KC là phân giác của \(\widehat {IKD}\). (đpcm)

Bài 7. Cho ΔABC vuông tại A, biết \(AB = 3cm,BC = 5cm\). Tia phân giác của \(\widehat {ABC}\) cắt AC tại D.

a) Vẽ tia Cx vuông góc với BD tại E và tia Cx cắt đường thẳng AB tại F.

Chứng minh $\Delta ABD\backsim \Delta EBC$.

b) Tia FD cắt BC tại H. Kẻ đường thẳng qua H và vuông góc với AB tại M.

Chứng minh \(MH.AB = FH.MB\).

Hướng dẫn:

a) Chứng minh $\Delta ABD\backsim \Delta EBC$ theo trường hợp góc – góc.

b) Chứng minh \(\Delta BFC\) cân tại B suy ra \(CA = FH\).

Chứng minh $\Delta MBH\backsim \Delta ABC$ (g.g) suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{AC}}\).

Từ đó suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{FH}}\) suy ra \(MH.AB = FH.MB\).

Lời giải

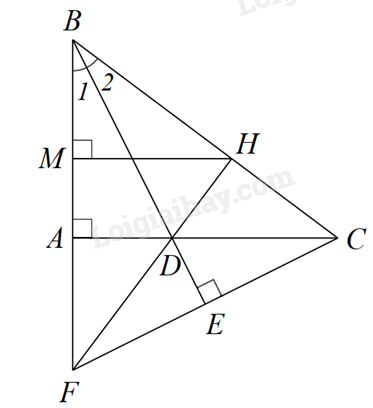
a) Chứng minh $\Delta ABD\backsim \Delta EBC$ theo trường hợp góc – góc.

Xét \(\Delta ABD\) và \(\Delta EBC\) có:

\(\widehat A = \widehat E = {90^0}\)

\(\widehat {{B_1}} = \widehat {{B_2}}\) (vì BE là tia phân giác của góc ABC)

Suy ra $\Delta ABD\backsim \Delta EBC$(g.g)

b) Tia FD cắt BC tại H. Kẻ đường thẳng qua H và vuông góc với AB tại M.

Chứng minh \(MH.AB = FH.MB\).

b) Chứng minh \(\Delta BFC\) cân tại B suy ra \(CA = FH\).

Chứng minh $\Delta MBH\backsim \Delta ABC$ (g.g) suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{AC}}\).

Từ đó suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{FH}}\) suy ra \(MH.AB = FH.MB\).

Xét tam giác BFC có BE vừa là tia phân giác vừa là đường cao của tam giác BFC nên tam giác BFC cân tại B.

Đường cao AC và BE của tam giác BFC cắt nhau tại D nên FH cũng là đường cao của tam giác BFC.

Mà tam giác BFC cân tại B nên đường cao AC = FH (1)

Xét \(\Delta MBH\) và \(\Delta ABC\) có:

\(\widehat M = \widehat A = {90^0}\)

\(\widehat B\) chung

Suy ra $\Delta MBH\backsim \Delta ABC$ (g.g) suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{AC}}\).

Mà AC = FH (cmt)

Suy ra \(\frac{{BM}}{{BA}} = \frac{{MH}}{{FH}}\) suy ra \(MH.AB = FH.MB\) (đpcm).

Bài 8. Cho ΔABC vuông tại A có AB < AC , đường cao AH .

a) Chứng minh $\Delta HAC\backsim \Delta ABC$

b) Chứng minh \(H{A^2} = HB.HC\)

c) Gọi D và E lần lượt là trung điểm của AB, BC.

Chứng minh \(CH.CB = 4.D{E^2}\)

d) Gọi M là giao điểm của đường thẳng vuông góc với BC tại B và đường thẳng DE . Gọi N là giao điểm của AH và CM . Chứng minh N là trung điểm của AH.

Hướng dẫn:

a) Chứng minh $\Delta HAC\backsim \Delta ABC$ theo trường hợp góc – góc.

b) Chứng minh $\Delta HAC\backsim \Delta HBA$ suy ra \(\frac{{HA}}{{HB}} = \frac{{HC}}{{HA}}\) hay \(H{A^2} = HB.HC\).

c) Chứng minh $\Delta HAC\backsim \Delta ABC(g.g)$ suy ra \(A{B^2} = CH.CB\) và DE là đường trung bình của tam giác ABC nên \(DE = \frac{1}{2}AB\).

d) Gọi AC và BM cắt nhau tại I và DE cắt AH tại I.

Chứng mình BM = MI và \(\frac{{NH}}{{MB}} = \frac{{AN}}{{MI}}\) \( \Rightarrow NH = AN\).

Lời giải

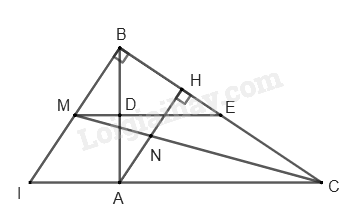
a) Xét tam giác HAC và tam giác ABC có:

\(\widehat A = \widehat H = {90^0}\)

\(\widehat C\) chung

Suy ra $\Delta HAC\backsim \Delta ABC$(g.g) (đpcm)

b) Xét \(\Delta HAC\) và \(\Delta HBA\) có:

\(\widehat {AHC} = \widehat {BHA} = {90^0}\)

\(\widehat {CAH} = \widehat {ABH}\) (cùng phụ với góc \(\widehat {ACH}\))

Suy ra $\Delta HAC\backsim \Delta HBA$ (g.g)

\( \Rightarrow \frac{{HA}}{{HB}} = \frac{{HC}}{{HA}} \Rightarrow H{A^2} = HB.HC\) (đpcm)

c) Vì $\Delta HAC\backsim \Delta ABC$(theo câu a)

\( \Rightarrow \frac{{AC}}{{BC}} = \frac{{HC}}{{AC}} \Rightarrow A{C^2} = HC.BC\)

Ta có:

D là trung điểm của AB

E là trung điểm của BC

Suy ra DE là đường trung bình của \(\Delta ABC\)

\( \Rightarrow AC = 2.DE \Rightarrow A{C^2} = 4.D{E^2}\)

Do đó \(HC \cdot BC = 4.D{E^2}\) (đpcm)

d) Gọi AC và BM cắt nhau tại I

Xét \(\Delta BIC\) có: \(ME//IC\) (do \(DE//AC\))

\( \Rightarrow \frac{{BE}}{{EC}} = \frac{{BM}}{{MI}} = 1 \Rightarrow BM = MI\)

Ta có \(AH \bot BC\) và \(BI \bot BC\) nên \(NH//BM\) và \(AN//MI\)

Xét \(\Delta CBM\) có \(NH//MB \Rightarrow \frac{{NH}}{{MB}} = \frac{{CN}}{{CM}}\) (1)

Xét \(\Delta CMI\) có \(AN//MI \Rightarrow \frac{{AN}}{{MI}} = \frac{{CN}}{{CM}}\) (2)

Từ (1), (2) \( \Rightarrow \frac{{NH}}{{MB}} = \frac{{AN}}{{MI}}\) mà \(MB = MI \Rightarrow NH = AN\) hay N là trung điểm của AH (đpcm).

Bài 9. Một hộp chứa 6 tấm thẻ cùng loại được đánh số lần lượt là 2; 3; 5; 8; 13; 21. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Tính xác suất của các biến cố:

A: “Số ghi trên thẻ là số lẻ”.

B: “Số ghi trên thẻ là số nguyên tố”.

C: “Số ghi trên thẻ là số chính phương”.

Hướng dẫn:

Tính số kết quả thuận lợi cho biến cố A, B, C.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.

Lời giải

Có 6 kết quả có thể xảy ra khi lấy ngẫu nhiên 1 thẻ từ hộp, đó là: 2; 3; 5; 8; 13; 21.

+) Có 4 số lẻ là 3; 5; 13; 21 nên số kết quả thuận lợi cho biến cố A là 4.

Xác suất của biến cố A: “Số ghi trên thẻ là số lẻ” là: \(\frac{4}{6} = \frac{2}{3}\).

+) Có 4 số nguyên tố là: 2; 3; 5; 13 nên số kết quả thuận lợi cho biến cố B là 4.

Xác suất của biến cố B: “Số ghi trên thẻ là số nguyên tố” là: \(\frac{4}{6} = \frac{2}{3}\).

+) Không có số chính phương trong các số trên nên số kết quả thuận lợi cho biến cố C là 0.

Xác suất của biến cố C: “Số ghi trên thẻ là số chính phương” là: \(\frac{0}{6} = 0\).

Bài 10. Khuê tung hai đồng xu giống nhau 100 lần và ghi lại kết quả ở bảng sau:

Tính xác suất thực nghiệm của biến cố: “Hai đồng xu đều xuất hiện mặt sấp sau 100 lần tung”.

Hướng dẫn:

Xác suất thực nghiệm của biến cố bằng tỉ số giữa số lần xảy ra biến cố với tổng số lần thực nghiệm.

Lời giải

Vì Khuê tung hai đồng xu giống nhau 100 lần, có 16 lần hai đồng xu đều xuất hiện mặt sấp, do đó xác suất thực nghiệm của biến cố: “Hai đồng xu đều xuất hiện mặt sấp sau 100 lần tung” là:

\(\frac{{16}}{{100}} = \frac{4}{{25}}\).

Bài 11*. Giải phương trình \(\left( {3x – 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = – 16\)

Hướng dẫn:

Nhân cả hai vế của phương trình với 9, biến đối phương trình thành:

\(\left( {3x – 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = – 144\)

Đặt \(3x + 3 = t\), biến đổi \(3x – 2\) và \(3x + 8\) theo t.

Ta có phương trình ẩn t mới.

Giải phương trình để tìm t.

Lời giải

Ta có: \(\left( {3x – 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = – 16\)

Nhân cả hai vế của phương trình với 9, ta được:

\(\begin{array}{l}9.\left( {3x – 2} \right){\left( {x + 1} \right)^2}\left( {3x + 8} \right) = 9.\left( { – 16} \right)\\\left( {3x – 2} \right)\left[ {9{{\left( {x + 1} \right)}^2}} \right]\left( {3x + 8} \right) = 9.\left( { – 16} \right)\\\left( {3x – 2} \right){\left( {3x + 3} \right)^2}\left( {3x + 8} \right) = – 144\end{array}\)

Đặt \(3x + 3 = t \Rightarrow 3x – 2 = t – 5;3x + 8 = t + 5\)

Ta có phương trình:

\(\left( {t – 5} \right){t^2}\left( {t + 5} \right) = – 144\)

\(\begin{array}{l}{t^4} – 25{t^2} + 144 = 0\\\left( {{t^2} – 9} \right)\left( {{t^2} – 16} \right) = 0\\\left[ \begin{array}{l}{t^2} = 9\\{t^2} = 16\end{array} \right.\\\left[ \begin{array}{l}t = \pm 3\\t = \pm 5\end{array} \right.\end{array}\)

Ta có bảng sau:

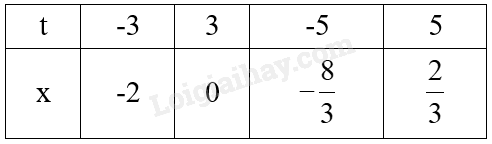
Vậy nghiệm của phương trình là \(x \in \left\{ { – 2;0; – \frac{8}{3};\frac{2}{3}} \right\}\).

Bài 12*. Cho các số thực a, b, c thỏa mãn abc = 2024. Tính giá trị của biểu thức:

\(P = \frac{{2bc – 2024}}{{3c – 2bc + 2024}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{4048 – 3ac}}{{3ac – 4048 + 2024a}}\)

Hướng dẫn:

Thay 2024 = abc và 4048 = 2abc, nhóm nhân tử chung để rút gọn các phân thức trong biểu thức.

Từ đó ta tính được giá trị của biểu thức.

Lời giải

Ta có:

\(\begin{array}{l}P = \frac{{2bc – 2024}}{{3c – 2bc + 2024}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{4048 – 3ac}}{{3ac – 4048 + 2024a}}\\ = \frac{{2bc – abc}}{{3c – 2bc + abc}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{2abc – 3ac}}{{3ac – 2abc + {a^2}bc}}\\ = \frac{{bc\left( {2 – a} \right)}}{{c\left( {3 – 2b + ab} \right)}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{ac\left( {2b – 3} \right)}}{{ac\left( {3 – 2b + ab} \right)}}\\ = \frac{{b\left( {2 – a} \right)}}{{3 – 2b + ab}} – \frac{{2b}}{{3 – 2b + ab}} + \frac{{2b – 3}}{{3 – 2b + ab}}\\ = \frac{{2b – ab – 2b + 2b – 3}}{{3 – 2b + ab}}\\ = \frac{{ – ab + 2b – 3}}{{3 – 2b + ab}}\\ = \frac{{ – \left( {3 – 2b + ab} \right)}}{{3 – 2b + ab}}\\ = – 1\end{array}\)

Vậy \(P = – 1\).

Bài 13*. Cho 2024 số: \({a_1},{a_2},…,{a_{2024}}\) với \({a_k} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}}\) \(\left( {k = 1,2,…,2024} \right)\).

Tính giá trị biểu thức \(A = {a_1} + {a_2} + … + {a_{2024}}\).

Hướng dẫn:

Phân tích \({a_k} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}} = \frac{1}{{{k^2}}} – \frac{1}{{{{\left( {k + 1} \right)}^2}}}\)

Từ đó tính \(A\).

Lời giải

Ta có:

\({a_k} = \frac{{2k + 1}}{{{{\left[ {k\left( {k + 1} \right)} \right]}^2}}} = \frac{{{{\left( {k + 1} \right)}^2} – {k^2}}}{{{k^2}{{\left( {k + 1} \right)}^2}}} = \frac{1}{{{k^2}}} – \frac{1}{{{{\left( {k + 1} \right)}^2}}}\)

Do đó:

\(\begin{array}{l}A = {a_1} + {a_2} + {a_3} + … + {a_{2024}}\\ = \left( {\frac{1}{{{1^2}}} – \frac{1}{{{2^2}}}} \right) + \left( {\frac{1}{{{2^2}}} – \frac{1}{{{3^2}}}} \right) + \left( {\frac{1}{{{3^2}}} – \frac{1}{{{4^2}}}} \right) + … + \left( {\frac{1}{{{{2023}^2}}} – \frac{1}{{{{2024}^2}}}} \right)\\ = 1 – \frac{1}{{{{2024}^2}}}\\ = \frac{{{{2024}^2} – 1}}{{{{2024}^2}}}\end{array}\)

Vậy \(A = \frac{{{{2024}^2} – 1}}{{{{2024}^2}}}\)