Tổng ba góc trong một tam giác bằng \({180^o}\). Lời giải bài tập, câu hỏi Giải bài 4 (4.10) trang 61 vở thực hành Toán 7 – Luyện tập chung trang 60 – 61 – 62. Bài 4 (4.10). Cho tam giác ABC có \(\widehat {BCA} = {60^o}\…
Đề bài/câu hỏi:
Bài 4 (4.10). Cho tam giác ABC có \(\widehat {BCA} = {60^o}\)và điểm M nằm trên cạnh BC sao cho \(\widehat {BAM} = {20^o},\widehat {AMC} = {80^o}\) . Tính số đo \(\widehat {AMB},\widehat {ABC},\widehat {BAC}\).
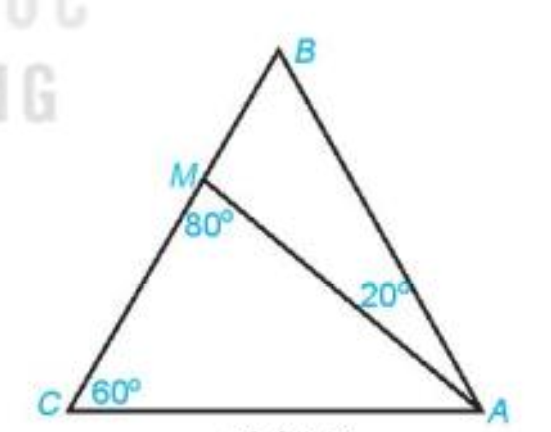
Hướng dẫn:
Tổng ba góc trong một tam giác bằng \({180^o}\).
Lời giải:
|
GT |
\(\Delta ABC,\widehat {BCA} = {60^o}\),\(\widehat {BAM} = {20^o},\widehat {AMC} = {80^o}\) |
|
KL |
Tính \(\widehat {AMB},\widehat {ABC},\widehat {BAC}\) |
Vì AMB và AMC là hai góc kề bù nên ta có
\(\widehat {AMB} + \widehat {AMC} = {180^o} \Rightarrow \widehat {AMB} = {180^o} – \widehat {AMC} = {100^o}\)
Tổng ba góc trong tam giác ABM bằng \({180^o}\)nên ta có
\(\widehat {ABM} + \widehat {AMB} + \widehat {BAM} = {180^o} \Rightarrow \widehat {ABM} = {180^o} – \widehat {AMB} – \widehat {BAM} = {180^o} – {100^o} – {20^o} = {60^o}\)
Vì M nằm trên cạnh BC nên \(\widehat {ABC} = \widehat {ABM} = {60^o}\)
Tổng ba góc trong tam giác ABC bằng \({180^o}\)nên ta có
\(\widehat {ABC} + \widehat {BCA} + \widehat {BAC} = {180^o} \Rightarrow \widehat {BAC} = {180^o} – \widehat {BCA} – \widehat {ABC} = {60^o}\)
Kết luận \(\widehat {AMB} = {100^o},\widehat {ABC} = {60^o},\widehat {BAC} = {60^o}\)