Tổng ba góc trong một tam giác bằng \({180^o}\). Giải và trình bày phương pháp giải Giải bài 2 (4.8) trang 60 vở thực hành Toán 7 – Luyện tập chung trang 60 – 61 – 62. Bài 2 (4.8). Tìm các số đo góc còn lại trong mỗi tam giác dưới đây….
Đề bài/câu hỏi:
Bài 2 (4.8). Tìm các số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.
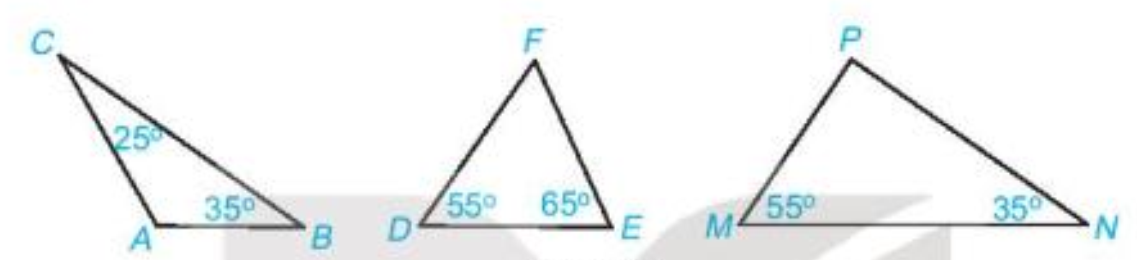
Hướng dẫn:
Tổng ba góc trong một tam giác bằng \({180^o}\).
Lời giải:
Vì tổng ba góc trong tam giác ABC bằng \({180^o}\)nên ta có
\(\widehat A + \widehat B + \widehat C = {180^o} \Rightarrow \widehat A = {180^o} – \widehat B – \widehat C = {180^o} – {25^o} – {35^o} = {120^o}\)
Tương tự tròn tam giác DFE ta có
\(\widehat D + \widehat E + \widehat F = {180^o} \Rightarrow \widehat F = {180^o} – \widehat D – \widehat E = {180^o} – {55^o} – {65^o} = {60^o}\)
Cuối cùng trong tam giác MNP ta có
\(\widehat M + \widehat N + \widehat P = {180^o} \Rightarrow \widehat P = {180^o} – \widehat M – \widehat N = {180^o} – {55^o} – {35^o} = {90^o}\)
Kết luận \(\widehat A = {120^o},\widehat F = {60^o},\widehat P = {90^o}\) và chỉ cótam giác MNP có một góc vuông nên chỉ có MNP là tam giác vuông.